如您所知，MetaTrader 5允许使用内置的基于两种算法的策略测试器优化交易策略：直接枚举输入参数和遗传算法-GA。遗传优化是一种进化算法，它提供了显著的过程加速。然而，遗传算法的结果在很大程度上取决于特定遗传算法实现的任务和细节，特别是测试人员提供的任务和细节。这就是为什么许多希望扩展标准功能的交易者试图为MetaTrader创建自己的优化器。在这里，可能的快速优化方法并不局限于遗传算法。除了遗传算法外，还有其他一些流行的方法，如模拟退火算法和粒子群优化算法。

在本文中，我们将实现粒子群优化（Particle Swarm Optimization，PSO）算法，并尝试将其集成到MetaTrader测试器中，以便在可用的本地代理上并行运行。目标优化函数将是用户选择的EA交易变量。

粒子群方法

从算法的角度来看，PSO方法相对简单。其主要思想是在EA交易的输入参数空间中生成一组虚拟“粒子”。然后，粒子移动并根据EA在空间中相应点的交易度量改变其速度。该过程重复多次，直到性能停止改善。该算法的伪代码如下：

粒子群优化伪码

根据这个代码，每个粒子都有一个当前的位置、速度和过去“最佳”点的记忆。这里，“最佳”点是指达到该粒子目标函数最高值的点（一组EA输入参数）。让我们在类里面描述一下。

  class Particle
  {
    public:
      double position[];    // current point
      double best[];        // best point known to the particle
      double velocity[];    // current speed
      
      double positionValue; // EA performance in current point
      double bestValue;     // EA performance in the best point
      int    group;
      
      Particle(const int params)
      {
        ArrayResize(position, params);
        ArrayResize(best, params);
        ArrayResize(velocity, params);
        bestValue = -DBL_MAX;
        group = -1;
      }
  };

所有数组的大小都等于优化空间的维数，因此它等于正在优化的专家顾问参数的数目（传递给构造函数）。默认情况下，目标函数值越大，优化效果越好。因此，用最小可能的 -DBL_MAX 数值来初始化 bestValue 字段。其中一个交易指标通常被用来作为评估EA的标准，如利润、盈利能力、夏普比率等。如果通过较低值被认为更好的参数，例如回撤，来执行优化，则可以进行适当的转换以最大化相反的值。

数组和变量是公有的，以简化访问和它们的重新计算代码。严格遵守OOP原则需要使用“private”修饰符隐藏它们，并描述读取和修改方法。

除了单个粒子外，该算法还处理所谓的“拓扑”或粒子子集。它们可以根据不同的原则来创建。“社会群体拓扑”将用于我们的案例。这样的组存储有关其所有粒子中最佳位置的信息。

  class Group
  {
    private:
      double result;    // best EA performance in the group
    
    public:
      double optimum[]; // best known position in the group
      
      Group(const int params)
      {
        ArrayResize(optimum, params);
        ArrayInitialize(optimum, 0);
        result = -DBL_MAX;
      }
      
      void assign(const double x)
      {
        result = x;
      }
      
      double getResult() const
      {
        return result;
      }
      
      bool isAssigned()
      {
        return result != -DBL_MAX;
      }
  };

通过在粒子类的“group”字段中指定组名，我们可以指示粒子所属的组（见上文）。

现在，让我们继续对粒子群算法本身进行编码。它将作为一个单独的类实现。让我们从粒子和群的数组开始。

  class Swarm
  {
    private:
      Particle *particles[];
      Group *groups[];
      int _size;             // number of particles
      int _globals;          // number of groups
      int _params;           // number of parameters to optimize

对于每个参数，我们需要指定执行优化的值的范围，以及增量（步长）。

      double highs[];
      double lows[];
      double steps[];

此外，最佳参数集应该存储在某个地方。

      double solution[];

因为类将有几个不同的构造函数，让我们来描述统一的初始化方法。

    void init(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[])
    {
      _size = size;
      _globals = globals;
      _params = params;
      
      ArrayCopy(highs, max);
      ArrayCopy(lows, min);
      ArrayCopy(steps, inc);
      
      ArrayResize(solution, _params);
      
      ArrayResize(particles, _size);
      for(int i = 0; i < _size; i++)          // loop through particles
      {
        particles[i] = new Particle(_params);
        
        ///do
        ///{
          for(int p = 0; p < _params; p++)    // loop through all dimensions
          {
            // random placement
            particles[i].position[p] = (MathRand() * 1.0 / 32767) * (highs[p] - lows[p]) + lows[p];
            // adjust it according to step granularity
            if(steps[p] != 0)
            {
              particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p];
            }
            // the only position is the best so far
            particles[i].best[p] = particles[i].position[p];
            // random speed
            particles[i].velocity[p] = (MathRand() * 1.0 / 32767) * 2 * (highs[p] - lows[p]) - (highs[p] - lows[p]);
          }
        ///}
        ///while(index.add(crc64(particles[i].position)) && !IsStopped());
      }
      
      ArrayResize(groups, _globals);
      for(int i = 0; i < _globals; i++)
      {
        groups[i] = new Group(_params);
      }
      
      for(int i = 0; i < _size; i++)
      {
        // random group membership
        particles[i].group = (_globals > 1) ?(int)MathMin(MathRand() * 1.0 / 32767 * _globals, _globals - 1) : 0;
      }
    }

所有的数组都是按照给定的维数分布的，并且被传输的数据填充。粒子的初始位置、速度和群成员是随机确定的。上面的代码中有一些重要的注释。我们稍后再谈这个。

请注意，粒子群算法的经典版本旨在优化连续坐标系中定义的函数。然而，EA参数通常是通过一定的步长来测试的。例如，标准移动平均线的周期不能为11.5。这就是为什么，除了所有维度的一系列可接受值之外，我们还设置了用于舍入粒子位置的步长。这不仅要在初始化阶段进行，而且要在优化过程中的计算中进行。

现在，我们可以使用 init 实现几个构造函数。

  #define AUTO_SIZE_FACTOR 5
  
  public:
    Swarm(const int params, const double &max[], const double &min[], const double &step[])
    {
      init(params * AUTO_SIZE_FACTOR, (int)MathSqrt(params * AUTO_SIZE_FACTOR), params, max, min, step);
    }
    
    Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[])
    {
      init(size, globals, params, max, min, step);
    }

第一种方法使用一个众所周知的经验法则，根据参数的个数来计算群的大小和群的个数。可以根据需要更改 AUTO_SIZE_FACTOR 常量（默认值为5）。第二个构造函数允许显式地指定所有值。

析构函数释放分配的内存。

    ~Swarm()
    {
      for(int i = 0; i < _size; i++)
      {
        delete particles[i];
      }
      for(int i = 0; i < _globals; i++)
      {
        delete groups[i];
      }
    }

现在是时候编写直接执行优化的类的主方法了。

    double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)

第一个参数 Functor &f 特别有趣。显然，在各种输入参数的优化过程中，将调用专家顾问，作为响应，将返回估计数（利润、盈利能力或其他特征）。粒子群对EA交易一无所知（也不应该知道任何事情）。它的唯一任务是找到一个未知的目标函数的最优值与一组任意的数值参数。这就是为什么我们使用抽象接口，即名为 Functor 的类。

  class Functor
  {
    public:
      virtual double calculate(const double &vector[]) = 0;
  };

唯一的方法接收参数数组并返回一个数字（所有类型都是double）。将来，EA 必须以某种方式实现从 Functor 派生的类，并在 calculate 方法中计算所需的变量。因此，“optimize”方法的第一个参数将接收一个对象，该对象带有交易机器人提供的回调函数。

“optimize”方法的第二个参数是运行算法的最大循环数。以下3个参数设置粒子群优化系数：“inertia”-保持粒子的速度（速度通常随着值小于1而减小），“selfBoost”和“groupBoost”确定粒子在调整其方向到分词/组历史中最已知位置时的响应程度。

现在我们已经考虑了所有的参数，我们可以继续算法。优化循环几乎以某种简化的形式完全复制伪代码。

    double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
    {
      double result = -DBL_MAX;
      ArrayInitialize(solution, 0);
      
      for(int c = 0; c < cycles && !IsStopped(); c++)   // predefined number of cycles
      {
        for(int i = 0; i < _size && !IsStopped(); i++)  // loop through all particles
        {
          for(int p = 0; p < _params; p++)              // update particle position and speed
          {
            double r1 = MathRand() * 1.0 / 32767;
            double rg = MathRand() * 1.0 / 32767;
            particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]);
            particles[i].position[p] = particles[i].position[p] + particles[i].velocity[p];
            
            // make sure to keep the particle inside the boundaries of parameter space
            if(particles[i].position[p] < lows[p]) particles[i].position[p] = lows[p];
            else if(particles[i].position[p] > highs[p]) particles[i].position[p] = highs[p];
            
            // respect step size
            if(steps[p] != 0)
            {
              particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p];
            }
          }
          
          // get the function value for the particle i
          particles[i].positionValue = f.calculate(particles[i].position);
          
          // update the particle's best value and position (if improvement is found)          
          if(particles[i].positionValue > particles[i].bestValue)
          {
            particles[i].bestValue = particles[i].positionValue;
            ArrayCopy(particles[i].best, particles[i].position);
          }
          
          // update the group's best value and position (if improvement is found)          
          if(particles[i].positionValue > groups[particles[i].group].getResult())
          {
            groups[particles[i].group].assign(particles[i].positionValue);
            ArrayCopy(groups[particles[i].group].optimum, particles[i].position);
            
            // update the global maximum value and solution (if improvement is found)          
            if(particles[i].positionValue > result)
            {
              result = particles[i].positionValue;
              ArrayCopy(solution, particles[i].position);
            }
          }
        }
      }
      
      return result;
    }

该方法返回找到的目标函数的最大值。另一种方法用于读取坐标（参数集）。

    bool getSolution(double &result[])
    {
      ArrayCopy(result, solution);
      return !IsStopped();
    }

这几乎就是整个算法。我之前提到过一些简化。首先，考虑以下具体特性。

没有重复的离散世界

Functor 被多次调用以动态地重新计算参数集，但不能保证算法不会多次命中同一点，特别是考虑到沿轴的离散性。为了防止遇到这种巧合情况，有必要以某种方式确定已经计算的点并跳过它们。

参数只是数字或字节序列。最著名的检查数据唯一性的技术是使用散列（hash）。最流行的获取散列的方法是CRC。CRC是基于数据生成的校验数（通常是整数，多位），其方式使得来自数据集的两个这样的特征数的匹配很可能意味着这些集是相同的。CRC中的位数越多，匹配的概率就越高（几乎达到100%）对于我们的任务来说，64位CRC就足够了。如果需要，可以将其扩展或更改为另一个散列函数。CRC计算实现可以很容易地从 C 移植到 MQL。下面附带的 crc64.mqh 文件中提供了一个可能的选项。主要工作函数有以下原型。

  ulong crc64(ulong crc, const uchar &s[], int l);

它接受来自上一个数据块的CRC（如果它们不止一个，或者如果有一个块，则指定0）、字节数组和关于应该处理其中多少元素的信息。函数返回64位CRC。

我们需要在这个函数中输入一组参数。但这不能直接完成，因为每个参数都是双精度的。要将其转换为字节数组，让我们使用TypeToBytes.mqh库（文件附在文章后面；不过，最好检查代码库的最新版本）。

包含此库后，可以创建一个包装函数，从参数数组计算CRC64：

  #include <TypeToBytes.mqh>
  #include <crc64.mqh>
  
  template<typename T>
  ulong crc64(const T &array[])
  {
    ulong crc = 0;
    int len = ArraySize(array);
    for(int i = 0; i < len; i++)
    {
      crc = crc64(crc, _R(array[i]).Bytes, sizeof(T));
    }
    return crc;
  }

现在出现了以下问题：散列存储在哪里以及如何检查其唯一性。最合适的解决方案是二叉树。它是一种数据结构，提供了添加新值和检查已添加值是否存在的快速操作。高速是由称为平衡的特殊树属性提供的。换言之，树必须保持平衡（它必须始终保持在平衡状态），以确保操作的最大速度。这样我们就使用树来存储散列。这里是散列的定义。

哈希函数（哈希生成算法）为任何输入数据生成均匀分布的输出值。结果，在二叉树中添加hash在统计上使其状态接近平衡，从而导致高效率。

二叉树是节点的集合，每个节点都包含一个特定的值和两个对所谓的右节点和左节点的可选引用。左侧节点中的值始终小于父节点中的值；右侧节点中的值始终大于父节点中的值。通过比较新值和节点值，树从根开始填充。如果新值等于根（或其他节点）的值，则返回树中存在值的符号。如果新值小于节点中的值，则通过引用转到左侧节点，并以类似的方式处理其子树。如果新值大于节点中的值，就跟随右子树。如果有任何引用为空值（意味着没有其他分支），则搜索将在没有结果的情况下完成。因此，应该创建一个具有新值的新节点，而不是空引用。

已经创建了一对模板类来实现这个逻辑：TreeNode 和 BinaryTree。它们的完整代码在所附的头文件中提供。

  template<typename T>
  class TreeNode
  {
    private:
      TreeNode *left;
      TreeNode *right;
      T value;
  
    public:
      TreeNode(T t): value(t) {}
      // adds new value into subtrees and returns false or
      // returns true if t exists as value of this node or in subtrees
      bool add(T t);
      ~TreeNode();
      TreeNode *getLeft(void) const;
      TreeNode *getRight(void) const;
      T getValue(void) const;
  };
    
  template<typename T>
  class BinaryTree
  {
    private:
      TreeNode<T> *root;
      
    public:
      bool add(T t);
      ~BinaryTree();
  };

如果树中已经存在值，“add”方法返回 true。如果之前不存在，但刚刚添加，则返回 false。删除树的析构函数中的根会自动导致删除所有子节点。

实现的树类是最简单的变体之一。还有其他更高级的树，所以如果您愿意，可以尝试嵌入它们。

让我们向 Swarm 类添加 BinaryTree。

  class Swarm
  {
    private:
      BinaryTree<ulong> index;

“optimize”方法将粒子移动到新位置的部分应该扩展。

      double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
      {
        // ...
        
        double next[];
        ArrayResize(next, _params);
  
        for(int c = 0; c < cycles && !IsStopped(); c++)
        {
          int skipped = 0;
          for(int i = 0; i < _size && !IsStopped(); i++)
          {
            // new placement of particles using temporary array next
            for(int p = 0; p < _params; p++)
            {
              double r1 = MathRand() * 1.0 / 32767;
              double rg = MathRand() * 1.0 / 32767;
              particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]);
              next[p] = particles[i].position[p] + particles[i].velocity[p];
              if(next[p] < lows[p]) next[p] = lows[p];
              else if(next[p] > highs[p]) next[p] = highs[p];
              if(steps[p] != 0)
              {
                next[p] = ((int)MathRound(next[p] / steps[p])) * steps[p];
              }
            }
  
            // check if the tree contains this parameter set and add it if not
            if(index.Add(crc64(next)))
            {
              skipped++;
              continue;
            }
  
            // apply new position to the particle
            ArrayCopy(particles[i].position, next);
            
            particles[i].positionValue = f.calculate(particles[i].position);
            
            // ...
          }
          Print("Cycle ", c, " done, skipped ", skipped, " of ", _size, " / ", result);
          if(skipped == _size) break; // full coverage
        }

我们已经添加了辅助数组'next'，其中首先添加新创建的坐标。为它们计算CRC并检查值的唯一性。如果尚未遇到新位置，则会将其添加到树中，复制到相应的粒子，并对此位置执行所有必要的计算。如果位置已经存在于树中（即，functor 已经被计算出来），则跳过此迭代。

测试基本功能

上面讨论的所有内容都是运行第一个测试的最低必要基础。让我们使用 testpso.mq5 脚本以确保优化真正起作用。头文件 ParticleSwarmParallel.mqh 这个脚本中使用的头文件不仅包含已经熟悉的类，还包含我们将在下面考虑的其他改进。

这些测试是以OOP风格设计的，它允许您设置自己喜欢的目标函数。测试的基类是 BaseFunctor。

    class BaseFunctor: public Functor
    {
      protected:
        const int params;
        double max[], min[], steps[];
        
      public:
        BaseFunctor(const int p): params(p) // number of parameters
        {
          ArrayResize(max, params);
          ArrayResize(min, params);
          ArrayResize(steps, params);
          ArrayInitialize(steps, 0);
          
          PSOTests::register(&this);
        }
        
        virtual void test(const int loop)   // worker method
        {
          Swarm swarm(params, max, min, steps);
          swarm.optimize(this, loop);
          double result[];
          swarm.getSolution(result);
          for(int i = 0; i < params; i++)
          {
            Print(i, " ", result[i]);
          }
        }
    };

派生类的所有对象将在创建时使用 PSOTests 类中的“register”方法自动注册自己。

  class PSOTests
  {
      static BaseFunctor *testCases[];
    
    public:
      static void register(BaseFunctor *f)
      {
        int n = ArraySize(testCases);
        ArrayResize(testCases, n + 1);
        testCases[n] = f;
      }
      
      static void run(const int loop = 100)
      {
        for(int i = 0; i < ArraySize(testCases); i++)
        {
          testCases[i].test(loop);
        }
      }
  };

测试（优化）由“run”方法运行，该方法对所有注册对象调用“test”。

脚本中实现了许多流行的基准函数，包括“rosenbrock”、“griewank”、“sphere”。例如，sphere（球体）的搜索范围和“calculate”方法可以定义如下。

      class Sphere: public BaseFunctor
      {
        public:
          Sphere(): BaseFunctor(3) // expected global minimum (0, 0, 0)
          {
            for(int i = 0; i < params; i++)
            {
              max[i] = 100;
              min[i] = -100;
            }
          }
          
          virtual void test(const int loop)
          {
            Print("Optimizing " + typename(this));
            BaseFunctor::test(loop);
          }
          
          virtual double calculate(const double &vec[])
          {
            int dim = ArraySize(vec);
            double sum = 0;
            for(int i = 0; i < dim; i++) sum += pow(vec[i], 2);
            return -sum; // negative for maximization
          }
      };

注意，标准基准函数使用最小化，而我们实现了一个基于最大化的算法（因为我们的目标是搜索最大的EA性能）。因此，计算结果将使用负号。此外，我们这里不使用离散步骤，因此函数是连续的。

  void OnStart()
  {
    PSOTests::Sphere sphere;
    PSOTests::Griewank griewank;
    PSOTests::Rosenbrock rosenbrock;
    PSOTests::run();
  }

通过运行脚本，可以看到它记录的坐标值接近精确解（极值）。因为粒子是随机初始化的，所以每次运行都会产生稍微不同的值。解的精度取决于算法的输入参数。

  Optimizing PSOTests::Sphere
  PSO[3] created: 15/3
  PSO Processing...
  Cycle 0 done, skipped 0 of 15 / -1279.167775306995
  Cycle 10 done, skipped 0 of 15 / -231.4807406906516
  Cycle 20 done, skipped 0 of 15 / -4.269510657558273
  Cycle 30 done, skipped 0 of 15 / -1.931949742316357
  Cycle 40 done, skipped 0 of 15 / -0.06018744740061506
  Cycle 50 done, skipped 0 of 15 / -0.009498109984732127
  Cycle 60 done, skipped 0 of 15 / -0.002058433538555499
  Cycle 70 done, skipped 0 of 15 / -0.0001494176502579518
  Cycle 80 done, skipped 0 of 15 / -4.141817579039349e-05
  Cycle 90 done, skipped 0 of 15 / -1.90930142126799e-05
  Cycle 99 done, skipped 0 of 15 / -8.161728746514931e-07
  PSO Finished 1500 of 1500 planned calculations: true
  0 -0.000594423827318461
  1 -0.000484001094843528
  2 0.000478096358862763
  Optimizing PSOTests::Griewank
  PSO[2] created: 10/3
  PSO Processing...
  Cycle 0 done, skipped 0 of 10 / -26.96927938978973
  Cycle 10 done, skipped 0 of 10 / -0.939220906325796
  Cycle 20 done, skipped 0 of 10 / -0.3074442362962919
  Cycle 30 done, skipped 0 of 10 / -0.121905607345751
  Cycle 40 done, skipped 0 of 10 / -0.03294107382891465
  Cycle 50 done, skipped 0 of 10 / -0.02138355984774098
  Cycle 60 done, skipped 0 of 10 / -0.01060479828529859
  Cycle 70 done, skipped 0 of 10 / -0.009728742850384609
  Cycle 80 done, skipped 0 of 10 / -0.008640623678293768
  Cycle 90 done, skipped 0 of 10 / -0.008578769833161193
  Cycle 99 done, skipped 0 of 10 / -0.008578769833161193
  PSO Finished 996 of 1000 planned calculations: true
  0 3.188612982502877
  1 -4.435728146291838
  Optimizing PSOTests::Rosenbrock
  PSO[2] created: 10/3
  PSO Processing...
  Cycle 0 done, skipped 0 of 10 / -19.05855349617553
  Cycle 10 done, skipped 1 of 10 / -0.4255148824156119
  Cycle 20 done, skipped 0 of 10 / -0.1935391314277153
  Cycle 30 done, skipped 0 of 10 / -0.006468452482022688
  Cycle 40 done, skipped 0 of 10 / -0.001031992354315317
  Cycle 50 done, skipped 0 of 10 / -0.00101322411502283
  Cycle 60 done, skipped 0 of 10 / -0.0008800704421316765
  Cycle 70 done, skipped 0 of 10 / -0.0005593151578155307
  Cycle 80 done, skipped 0 of 10 / -0.0005516786893301249
  Cycle 90 done, skipped 0 of 10 / -0.0005473814163781119
  Cycle 99 done, skipped 0 of 10 / -7.255520122486163e-06
  PSO Finished 982 of 1000 planned calculations: true
  0 1.001858172119364
  1 1.003524791491219

请注意，群大小和组数（写入PSO[N]创建的登录行：X/G，其中N是空间维度，X是粒子数，G是组数）是根据基于输入数据的编程经验规则自动选择的。

走向一个并行的世界

第一次测试很好。然而，它有一个细微差别-粒子计数周期是在一个线程中执行的，而终端允许使用所有处理器内核。我们的最终目标是编写一个PSO优化引擎，该引擎可以内置到 EA 交易中，在 MetaTrader 测试程序中进行多线程优化，从而为标准遗传算法提供一种替代方法。

通过在EA中而不是脚本中机械地传输算法，计算无法并行化。这需要修改算法。

如果查看现有代码，此任务建议选择粒子组进行并行计算。每组都可以独立处理。在每组内执行指定次数的完整循环。

为了避免修改“Swarm”类的核心，让我们使用一个简单的解决方案：我们将创建几个类实例，而不是一个类中的几个组，每个类实例中的组数将退化，即等于一个。此外，我们需要提供一个允许实例交换信息的代码，因为每个实例将在其自己的测试代理上执行。

首先，让我们添加一种新的对象初始化方式。

    Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[])
    {
      if(MQLInfoInteger(MQL_OPTIMIZATION))
      {
        init(size == 0 ? params * AUTO_SIZE_FACTOR : size, 1, params, max, min, step);
      }
      ...

根据优化模式下的程序操作，将组数设置为1。默认群集大小由经验法则确定（除非“size”参数显式设置为0以外的值）。

在OnTester事件处理程序中，EA交易将能够使用 getSolution 函数获得一个小型群（仅由一个组组成）的结果，并将其以帧的形式发送到终端。终端可以分析过程并选择最佳的过程。从逻辑上讲，并行群/组的数量应至少等于核心的数量。但是，它可以更高（尽管您应该尝试将其设置为核心数的倍数）。空间的尺寸越大，可能需要更多的组。但是核心的数量应该足够简单的测试。

为了计算没有重复点的空间，需要在实例之间进行数据交换。正如您所记得的，每个对象中处理点的列表存储在“index”二叉树中。它可以以帧的形式发送到终端，与结果类似，但问题是这些列表的假设组合注册表不能发送回测试代理。不幸的是，测试器架构只支持从代理到终端的受控数据传输，而不支持从终端到代理的受控数据传输。来自终端的任务以封闭格式分发给代理。

因此，我决定只使用本地代理，并将每个组的索引保存到一个共享文件夹（FILE_COMMON）中的文件。每个代理编写自己的索引，可以随时读取所有其他过程的索引，也可以将它们添加到自己的索引中。在过程初始化期间可能需要这样做。

对编写索引的支持是使用众所周知的“visitor”模式实现的。

  template<typename T>
  class Visitor
  {
    public:
      virtual void visit(TreeNode<T> *node) = 0;
  };

它的极简接口声明我们将对传递的树节点执行一些任意操作。已经为使用文件创建了一个特定的后续实现：Exporter。每个节点的内部值按引用遍历整个树的顺序存储在文件中的单独一行中。

  template<typename T>
  class Exporter: public Visitor<T>
  {
    private:
      int file;
      uint level;
      
    public:
      Exporter(const string name): level(0)
      {
        file = FileOpen(name, FILE_READ | FILE_WRITE | FILE_CSV | FILE_ANSI | FILE_SHARE_READ| FILE_SHARE_WRITE | FILE_COMMON, ',');
      }
      
      ~Exporter()
      {
        FileClose(file);
      }
      
      virtual void visit(TreeNode<T> *node) override
      {
        #ifdef PSO_DEBUG_BINTREE
        if(node.getLeft()) visit(node.getLeft());
        FileWrite(file, node.getValue());
        if(node.getRight()) visit(node.getRight());
        #else
        const T v = node.getValue();
        FileWrite(file, v);
        level++;
        if((level | (uint)v) % 2 == 0)
        {
          if(node.getLeft()) visit(node.getLeft());
          if(node.getRight()) visit(node.getRight());
        }
        else
        {
          if(node.getRight()) visit(node.getRight());
          if(node.getLeft()) visit(node.getLeft());
        }
        level--;
        #endif
      }
  };

有序树遍历似乎是最符合逻辑的，如果需要接收文件中的排序行以进行上下文比较，则只能用于调试目的。此方法由 PSO_DEBUG_BINTREE 条件编译指令包围，默认情况下禁用。实际上，树的统计平衡是通过添加存储在树中的随机、均匀分布的值（散列）来保证的。如果树元素以排序的形式保存，那么在从文件上传的过程中，我们将得到最次优和最慢的配置（一个长分支或一个列表）。为了避免这种情况，在树保存阶段引入了一种不确定性，即节点处理的顺序。

将树保存到传递的 visitor 的特殊方法可以使用 Exporter 类轻松地添加到 BinaryTree 类中。

  template<typename T>
  class BinaryTree
  {
      ...
      void visit(Visitor<T> *visitor)
      {
        visitor.visit(root);
      }
  };

Swarm类中的新方法也需要运行该操作。

    void exportIndex(const int id)
    {
      const string name = sharedName(id);
      Exporter<ulong> exporter(name);
      index.visit(&exporter);
    }

“id”参数表示唯一的过程编号（等于组号）。此参数将用于在测试器中配置优化。exportIndex方法应该在执行两个swarm方法之后立即调用：optimize 和 getSolution。这是由一个调用代码执行的，因为它可能并不总是必需的：我们的第一个“并行”示例（请进一步参阅）并不需要它。如果组的数量等于核心的数量，它们将无法交换任何信息，因为它们将并行启动，并且读取循环中的文件是没有效率的。

exportIndex 中提到的 sharedName 辅助函数允许基于组号、EA名称和终端文件夹创建唯一的名称。

  #define PPSO_FILE_PREFIX "PPSO-"
  
  string sharedName(const int id, const string prefix = PPSO_FILE_PREFIX, const string ext = ".csv")
  {
    ushort array[];
    StringToShortArray(TerminalInfoString(TERMINAL_PATH), array);
    const string program = MQLInfoString(MQL_PROGRAM_NAME) + "-";
    if(id != -1)
    {
      return prefix + program + StringFormat("%08I64X-%04d", crc64(array), id) + ext;
    }
    return prefix + program + StringFormat("%08I64X-*", crc64(array)) + ext;
  }

如果将等于 -1 的标识符传递给函数，函数将创建一个掩码来查找此终端实例的所有文件。当删除旧的临时文件（从这个专家顾问以前的优化中）以及读取并行流的索引时，使用此功能。这就是如何做到的。

      bool restoreIndex()
      {
        string name;
        const string filter = sharedName(-1); // use wildcards to merge multiple indices for all cores
        long h = FileFindFirst(filter, name, FILE_COMMON);
        if(h != INVALID_HANDLE)
        {
          do
          {
            FileReader reader(name, FILE_COMMON);
            reader.read(this);
          }
          while(FileFindNext(h, name));
          FileFindClose(h);
        }
        return true;
      }

找到的每个文件都传递给一个新的 FileReader 类进行处理。类负责以读取模式打开文件。它还按顺序加载所有行，并立即将它们传递给 Feed 接口。

  class Feed
  {
    public:
      virtual bool feed(const int dump) = 0;
  };
  
  class FileReader
  {
    protected:
      int dump;
      
    public:
      FileReader(const string name, const int flags = 0)
      {
        dump = FileOpen(name, FILE_READ | FILE_CSV | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags, ',');
      }
      
      virtual bool isReady() const
      {
        return dump != INVALID_HANDLE;
      }
      
      virtual bool read(Feed &pass)
      {
        if(!isReady()) return false;
        
        while(!FileIsEnding(dump))
        {
          if(!pass.feed(dump))
          {
            return false;
          }
        }
        return true;
      }
  };

正如您可能猜到的，Feed 接口必须直接在 Swarm 中实现，因为我们在 FileReader 中传递了这个接口。

  class Swarm: public Feed
  {
    private:
      ...
      int _read;
      int _unique;
      int _restored;
      BinaryTree<ulong> merge;
      
    public:
      ...
      virtual bool feed(const int dump) override
      {
        const ulong value = (ulong)FileReadString(dump);
        _read++;
        if(!index.add(value)) _restored++;    // just added into the tree
        else if(!merge.add(value)) _unique++; // was already indexed, hitting _unique in total
        return true;
      }
      ...

使用变量 _read、_unique 和 _restored，该方法计算读取的元素总数（从所有文件）、添加到索引的元素数和尚未添加的元素数（已经在索引中）。由于组独立运行，不同组的索引可以有重复项。

这些统计数据对于确定搜索空间何时被充分利用或接近被充分利用非常重要。在这种情况下，_unique 的数量接近可能的参数组合的数量。

随着完成的过程数的增加，共享历史中越来越多的唯一点将加载到本地索引中。在下一次执行“calculate”之后，索引将接收新的检查点，并且保存的文件的大小将不断增长。逐渐地，文件中的重叠元素将开始增加，这将需要一些额外的成本，但这比重新计算EA的交易活动要少。这将导致 PSO 周期的加速，处理每个后续组（测试任务），因为处理接近优化空间的全覆盖。

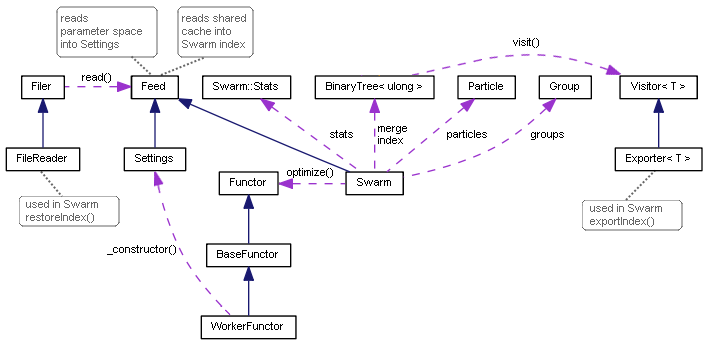
粒子群优化类图

并行计算测试

为了在多线程中测试算法性能，让我们将旧脚本转换为 PPSO.mq5 EA交易。它将在数学计算模式下运行，因为还不需要交易环境。

测试目标函数集是相同的，实现它们的类实际上是不变的。将在输入变量中选择一个特定的测试。

  enum TEST
  {
    Sphere,
    Griewank,
    Rosenbrock
  };
  
  sinput int Cycles = 100;
  sinput TEST TestCase = Sphere;
  sinput int SwarmSize = 0;
  input int GroupCount = 0;

在这里，我们还可以指定循环数、群大小和组数。所有这些都在 Functor 实现中使用，特别是在 Swarm 构造函数中。默认零值表示根据任务的维度自动选择。

  class BaseFunctor: public Functor
  {
    protected:
      const int params;
      double max[], min[], steps[];
      
      double optimum;
      double result[];
  
    public:
      ...
      virtual void test()
      {
        Swarm swarm(SwarmSize, GroupCount, params, max, min, steps);
        optimum = swarm.optimize(this, Cycles);
        swarm.getSolution(result);
      }
      
      double getSolution(double &output[]) const
      {
        ArrayCopy(output, result);
        return optimum;
      }
  };

所有计算都从 OnTester 处理程序开始。GroupCount 参数（测试器的迭代将通过它来组织）用作随机化器，以确保不同线程中的实例包含不同的粒子。根据 TestCase 参数创建测试 functor。接下来调用 functor.test() 方法，然后可以使用 functor.getSolution()，并且可以以帧的形式发送到终端。

  double OnTester()
  {
    MathSrand(GroupCount); // reproducible randomization
    
    BaseFunctor *functor = NULL;
    
    switch(TestCase)
    {
      case Sphere:
        functor = new PSOTests::Sphere();
        break;
      case Griewank:
        functor = new PSOTests::Griewank();
        break;
      case Rosenbrock:
        functor = new PSOTests::Rosenbrock();
        break;
    }
    
    functor.test();
    
    double output[];
    double result = functor.getSolution(output);
    if(MQLInfoInteger(MQL_OPTIMIZATION))
    {
      FrameAdd("PSO", 0xC0DE, result, output);
    }
    else
    {
      Print("Solution: ", result);
      for(int i = 0; i < ArraySize(output); i++)
      {
        Print(i, " ", output[i]);
      }
    }
    
    delete functor;
    return result;
  }

还有一系列函数，如 OnTesterInit，OnTesterPass，OnTesterDeinit 在终端中工作。它收集帧并从发送的帧中确定最佳解决方案。

  int passcount = 0;
  double best = -DBL_MAX;
  double location[];
  
  void OnTesterPass()
  {
    ulong pass;
    string name;
    long id;
    double r;
    double data[];
    
    while(FrameNext(pass, name, id, r, data))
    {
      // compare r with all other passes results
      if(r > best)
      {
        best = r;
        ArrayCopy(location, data);
      }
    
      Print(passcount, " ", id);
      
      const int n = ArraySize(data);
      ArrayResize(data, n + 1);
      data[n] = r;
      ArrayPrint(data, 12);
    
      passcount++;
    }
  }
  
  void OnTesterDeinit()
  {
    Print("Solution: ", best);
    ArrayPrint(location);
  }

将以下数据写入日志：pass 计数器、其序列号（在复杂任务上可能不同，当一个线程由于数据差异而超过另一个线程时）、目标函数的值和相应的参数。最后的决定是在 OnTesterDeinit 中作出的。

我们还可以让 EA 交易不仅在测试器中运行，而且在常规图表上运行。在这种情况下，PSO 算法将以常规的单线程模式执行。

  int OnInit()
  {
    if(!MQLInfoInteger(MQL_TESTER))
    {
      EventSetTimer(1);
    }
    return INIT_SUCCEEDED;
  }
  
  void OnTimer()
  {
    EventKillTimer();
    OnTester();
  }

让我们看看它是如何工作的。将使用以下输入参数值：

• Cycles — 100;
• TestCase — Griewank;
• SwarmSize — 100;
• GroupCount — 10;

在启动图表上的EA交易时，将出现以下日志。

  Successive PSO of Griewank
  PSO[2] created: 100/10
  PSO Processing...
  Cycle 0 done, skipped 0 of 100 / -1.000317162069485
  Cycle 10 done, skipped 0 of 100 / -0.2784790501384311
  Cycle 20 done, skipped 0 of 100 / -0.1879188508394087
  Cycle 30 done, skipped 0 of 100 / -0.06938172138150922
  Cycle 40 done, skipped 0 of 100 / -0.04958694402304631
  Cycle 50 done, skipped 0 of 100 / -0.0045818974357138
  Cycle 60 done, skipped 0 of 100 / -0.0045818974357138
  Cycle 70 done, skipped 0 of 100 / -0.002161613760466419
  Cycle 80 done, skipped 0 of 100 / -0.0008991629607246754
  Cycle 90 done, skipped 0 of 100 / -1.620636881582982e-05
  Cycle 99 done, skipped 0 of 100 / -1.342285474092986e-05
  PSO Finished 9948 of 10000 planned calculations: true
  Solution: -1.342285474092986e-05
  0 0.004966759354110293
  1 0.002079707592422949

由于测试用例的计算速度很快（一两秒钟之内），因此测量时间是没有意义的。这将添加到以后的实际交易任务中。

现在，在测试器中选择EA，在“Modeling”列表中设置“Math calculations”，对EA使用上述参数，GroupCount除外。此参数将用于优化。因此，设置初始值和最终值，比如0和3，步长为1，生成4个组（等于核心数）。所有群体的规模将是100（SwarmSize，整个群体）。如果处理器内核的数量足够（如果所有组在代理上并行工作），这应该不会影响性能，但会通过额外检查优化空间来提高解决方案的准确性。可以接收到以下日志：

  Parallel PSO of Griewank
  -12.550070232909  -0.002332638407  -0.039510275469
  -3.139749741924  4.438437934965 -0.007396077598
   3.139620588383  4.438298282495 -0.007396126543
   0.000374731767 -0.000072178955 -0.000000071551
  Solution: -7.1550806279852e-08 (after 4 passes)
   0.00037 -0.00007

因此，我们确保PSO算法的并行修改在优化模式下可以在测试器中使用。但到目前为止，这只是一个使用数学计算的测试。接下来，让我们调整 PSO 来优化交易环境中的 EA 交易。

EA 交易虚拟化和优化（MetaTrader 5中的 MQL4 API）

为了使用 PSO 引擎优化 EA 交易，需要实现基于一组输入参数模拟历史交易并计算统计信息的 Functor。

这就引发了许多应用程序开发人员在编写自己的优化器和/或替代标准优化器时所面临的困境。如何提供一个交易环境，包括，首先，报价，以及帐户状态和交易档案？如果使用数学计算模式，我们需要以某种方式准备所需的数据，然后将其传递给 EA 交易（代理）。这需要开发一个API中间层，它“透明地”模拟许多交易功能——这将允许专家顾问与通常的在线模式类似地工作。

为了避免这种情况，我决定使用一个现有的虚拟交易解决方案，该解决方案完全用MQL创建，并使用标准的历史数据结构，特别是ticks和bar。这就是 Virtual 库，是由 fxsaber 开发的。它允许在线（例如，对于图表上的周期性自我优化）和在测试器中计算专家顾问对可用历史的虚拟通过。在后一种情况下，我们可以使用任何常用的报价模式（“每个报价”，“基于真实报价的每个报价”）甚至“一分钟OHLC”-快速但更粗略地估计系统（每分钟只有4个报价）。

在包括 Virtual.mqh 头文件（与必要的依赖项一起下载）到 EA 代码中，可以使用以下行轻松组织虚拟测试：

      MqlTick _ticks[];                                     // global array
      ...                                                   // copy/collect ticks[]
      VIRTUAL::Tester(_ticks, OnTick /*, TesterStatistics(STAT_INITIAL_DEPOSIT)*/ );
      Print(VIRTUAL::ToString(INT_MAX));                    // output virtual trades in the log
      const double result = TesterStatistics(STAT_PROFIT);  // get required performance meter
      VIRTUAL::ResetTickets();                              // optional
      VIRTUAL::Delete();                                    // optional

所有操作都由静态的 VIRTUAL:：Tester 方法执行。应将以下数据传递给此方法：预先填充的所需历史期间和详细信息的记号数组、指向 OnTick 函数的指针（如果包含从在线交易切换到虚拟交易的逻辑，则可以使用标准处理程序）和初始存款（可选-如果未指定存款，将使用当前账户余额。如果上面的片段放在OnTester处理程序中（我们将把它放在那里），测试器的初始存款就可以忽略了。要找出虚拟交易的结果，请调用熟悉的 TesterStatistics 函数，在连接库之后，该函数实际上是“重叠的”，就像许多其他 MQL API 函数一样（如果愿意，可以检查源代码）。这种“重叠”足够聪明，可以将调用委托给实际执行交易的原始内核函数。请注意，在虚拟交易期间，并非所有来自 TesterStatistics 的标准指标都在库中计算。

请注意，该库基于MetaTrader 4交易API。换句话说，它只适用于在代码中使用“旧”函数的 EA 交易，尽管它们是用 MQL5 编写的。多亏了同一作者（MT4Orders）的另一个著名库，它们可以在 MetaTrader 5 环境中运行。

测试将使用 ExprBot.mq5 版本 EA 修改，最初出现在计算数学表达式（第2部分）一文中。EA 是使用 MT4Orders 实现的。新版本名为 ExprBotPSO.mq5 文件，在附件中提供。

EA 交易使用解析器引擎根据表达式计算交易信号。其好处将在后面解释。交易策略是相同的：两个移动平均线的交叉，考虑指定的背离阈值。以下是 EA 设置以及信号表达式：

  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
  input string Variables = "Threshold=0.001";
  input int Fast = 10;

  input int Slow = 21;

如果您对如何将输入变量替换为表达式以及如何将内置的 EMA 函数与相应的指示符集成有任何疑问，我建议您阅读前面提到的文章。这种新版机器人使用同样的原理，它将会稍微做些改进。

除了我们将在后面讨论的信号输入参数外，EA还有用于管理虚拟测试和PSO算法的参数。

• VirtualTester — 启用虚拟测试和/或优化的标志；默认值为false，表示正常操作。
• Estimator — 用于执行优化的变量；默认值为STAT_PROFIT。
• InternalOptimization — 在虚拟模式下启用优化的标志；默认值为false，表示单次虚拟交易。True 就会初始化内部使用 PSO 方法优化。
• PSO_Enable — 启用/禁用 PSO.
• PSO_Cycles — 每个过程中PSO重新计算的周期数；值越大，PSO搜索质量越好，但单个过程在没有反馈（日志记录）的情况下执行的时间更长。
• PSO_SwarmSize — 粒子群大小；默认为0，表示根据参数数量自动进行经验选择。
• PSO_GroupCount — 组数；这是一个用于组织多个过程的增量参数-从0到核心/代理数的值开始，然后增加。
• PSO_RandomSeed — 随机化器；每个组中的组号都被添加到其中，因此它们的初始化方式都不同。

在 the VirtualTester 模式中，EA将 OnTick 中的报价收集到一个数组中。然后，在 OnTester 中，虚拟库使用这个数组进行交易，用一个特殊的设置标志调用同一个 OnTick 处理程序，允许用虚拟操作执行代码。

因此，对于每个递增的 PSO_GroupCount 值，使用 PSO_SwarmSize 粒子大小的群，执行 PSO_Cycles 次重新计算。因此，我们在优化空间中测试 PSO_GroupCount * PSO_Cycles * PSO_SwarmSize = N 个点。每个点都是交易系统的虚拟运行。

为了获得最佳的结果，使用试错法找到合适的PSO参数。对于N个测试，组件的数量可以改变。测试的最终数目将小于N，因为相同的点可以命中（记住，这些点存储在 swarm 的二叉树中）。

代理仅在发送下一个任务时交换数据。并行执行的任务还看不到彼此的结果，还可以计算几个相同的坐标，并具有一定的概率。

当然，ExprBotPSO EA 交易包括 functor 类，这些类通常与我们在前面的示例中探讨的类相似。其中包括“test”方法，它创建一个 swarm 实例，在其中执行优化，并将结果保存在成员变量中（optimum，result[]）。

  class BaseFunctor: public Functor
  {
    ...
    public:
      virtual bool test(void)
      {
        Swarm swarm(PSO_SwarmSize, PSO_GroupCount, params, max, min, steps);
        if(MQLInfoInteger(MQL_OPTIMIZATION))
        {
          if(!swarm.restoreIndex()) return false;
        }
        optimum = swarm.optimize(this, PSO_Cycles);
        swarm.getSolution(result);
        if(MQLInfoInteger(MQL_OPTIMIZATION))
        {
          swarm.exportIndex(PSO_GroupCount);
        }
        return true;
      }
  };

这是我们第一次看到前面几节中描述的 restoreIndex 和 exportIndex 方法的用法。EA 交易的优化任务通常需要大量的计算（参数和组，每个组是一个测试通过），所以代理将需要交换信息。

虚拟EA测试按照声明的顺序以“calculate”方法执行。在优化空间设置的初始化中使用了一个新类 - Settings。

  class WorkerFunctor: public BaseFunctor
  {
    string names[];
  
    public:
      WorkerFunctor(const Settings &s): BaseFunctor(s.size())
      {
        s.getNames(names);
        for(int i = 0; i < params; i++)
        {
          max[i] = s.get<double>(i, SET_COLUMN_STOP);
          min[i] = s.get<double>(i, SET_COLUMN_START);
          steps[i] = s.get<double>(i, SET_COLUMN_STEP);
        }
      }
  
      virtual double calculate(const double &vec[])
      {
        VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT));
        VIRTUAL::ResetTickets();
        const double r = TesterStatistics(Estimator);
        VIRTUAL::Delete();
        return r;
      }
  };

关键是要开始优化，用户将以通常的方式配置 EA 的输入参数。然而，swarm 算法仅将测试器用于并行任务（通过增加组数）。因此，EA应该能够读取优化参数的设置，将其保存到传输给每个代理的辅助文件中，在测试仪中重置这些设置，并按组号分配优化。Settings类将从辅助文件中读取参数。文件是“EA_name.mq5.csv”，应使用转义符连接。

  #define PPSO_SHARED_SETTINGS __FILE__ + ".csv"
  #property tester_file PPSO_SHARED_SETTINGS

您可以在附件中查看 Settings 类,它逐行读取CSV文件。文件应具有以下列：

  #define MAX_COLUMN 4
  #define SET_COLUMN_NAME  0
  #define SET_COLUMN_START 1
  #define SET_COLUMN_STEP  2
  #define SET_COLUMN_STOP  3

它们都存储在内部数组中，并可通过“get”方法按名称或索引使用。isVoid（）方法返回没有设置的指示（文件无法读取、为空或具有写入格式）。

设置是在 OnTesterInit 处理函数中被写入文件的（见下文）。

我建议手动创建一个空文件“EA_name.mq5.csv”的文件。否则，第一次优化运行可能会出现问题。

不幸的是，即使在第一次启动时自动创建此文件，它也不会将文件发送给代理，这就是为什么在代理上的EA初始化以 INIT_PARAMETERS_INCORRECT 错误结束的原因。重复的优化启动也不会发送它，因为测试器会缓存有关已连接资源的信息，并且在用户在测试仪设置的下拉列表中重新选择EA之前不会考虑新添加的文件。只有在这之后，才能更新文件并将其发送给代理。因此，提前创建文件更容易。

  string header[];
  
  void OnTesterInit()
  {
    int h = FileOpen(PPSO_SHARED_SETTINGS, FILE_ANSI|FILE_WRITE|FILE_CSV, ',');
    if(h == INVALID_HANDLE)
    {
      Print("FileSave error: ", GetLastError());
    }
    
    MqlParam parameters[];
    string names[];
    
    EXPERT::Parameters(0, parameters, names);
    for(int i = 0; i < ArraySize(names); i++)
    {
      if(ResetOptimizableParam<double>(names[i], h))
      {
        const int n = ArraySize(header);
        ArrayResize(header, n + 1);
        header[n] = names[i];
      }
    }
    FileClose(h); // 5008
    
    bool enabled;
    long value, start, step, stop;
    if(ParameterGetRange("PSO_GroupCount", enabled, value, start, step, stop))
    {
      if(!enabled)
      {
        const int cores = TerminalInfoInteger(TERMINAL_CPU_CORES);
        Print("PSO_GroupCount is set to default (number of cores): ", cores);
        ParameterSetRange("PSO_GroupCount", true, 0, 1, 1, cores);
      }
    }
    
    // remove CRC indices from previous optimization runs
    Swarm::removeIndex();
  }

另外一个函数 ResetOptimizableParam 用于搜索启用了优化标志的参数并重置这些标志。此外，在OnTesterInit中，我们使用fxsaber的Expert库记住这些参数的名称，这样可以更直观地显示结果。但是，之所以需要这个库，主要是因为为了调用 ParameterGetRange/ParameterSetRange 标准函数，应该提前知道名称，但是 MQL API 不允许您获取参数列表。这也将使代码更加通用，因此您将能够在没有特殊修改的情况下将此代码包含到任何EA中。

  template<typename T>
  bool ResetOptimizableParam(const string name, const int h)
  {
    bool enabled;
    T value, start, step, stop;
    if(ParameterGetRange(name, enabled, value, start, step, stop))
    {
      // disable all native optimization except for PSO-related params
      // preserve original settings in the file h
      if((StringFind(name, "PSO_") != 0) && enabled)
      {
        ParameterSetRange(name, false, value, start, step, stop);
        FileWrite(h, name, start, step, stop); // 5007
        return true;
      }
    }
    return false;
  }

在代理上执行的 OnInit 处理函数中，设置被读取到 Settings 全局对象，如下所示：

  Settings settings;
  
  int OnInit()
  {
      ...
      FileReader f(PPSO_SHARED_SETTINGS);
      if(f.isReady() && f.read(settings))
      {
        const int n = settings.size();
        Print("Got settings: ", n);
      }
      else
      {
        if(MQLInfoInteger(MQL_OPTIMIZATION))
        {
          Print("FileLoad error: ", GetLastError());
          return INIT_PARAMETERS_INCORRECT;
        }
        else
        {
          Print("WARNING!Virtual optimization inside single pass - slowest mode, debugging only");
        }
      }
      ...
  }

正如您稍后将看到的，该对象被传递给 OnTester 处理函数中创建的 WorkerFunctor 对象，在该对象中执行所有计算和优化。在开始计算之前，我们需要收集报价点(tick)，这是在OnTick处理函数中完成的。

  bool OnTesterCalled = false;
  
  void OnTick()
  {
    if(VirtualTester && !OnTesterCalled)
    {
      MqlTick _tick;
      SymbolInfoTick(_Symbol, _tick);
      const int n = ArraySize(_ticks);
      ArrayResize(_ticks, n + 1, n / 2);
      _ticks[n] = _tick;
      
      return; // skip all time scope and collect ticks
    }
    ...
    // trading goes on here
  }

为什么我们要使用上面的方法而不是直接在 OnTester 中调用 CopyTicksRange 函数？首先，这个函数只在每一报价模式下工作，而我们需要为快速的一分钟OHLC模式（每分钟4个报价点）提供支持。其次，由于某种原因，在 tick 生成模式下返回的数组的大小被限制为131072（在使用实际tick时没有这样的限制）。

OnTestCalled 变量最初等于false，因此将收集 tick 历史记录。在启动 PSO 之前，在 OnTester 中，晚些时候会把 OnTesterCalled 设为 true。然后 Swarm 对象将开始在循环中计算函子（functor），在循环中调用引用同一个 OnTick 的 VIRTUAL::Tester。这一次，OnTesterCalled 将等于 true，控制权将不转移到 tick 收集模式，而是转移到交易逻辑模式。这将在稍后考虑。将来，随着 PSO 库的进一步发展，通过替换库头文件中的 OnTick 处理程序，可能会出现简化与现有 EA 交易集成的机制。

在此之前，使用OnTester（简化形式）。

  double OnTester()
  {
    if(VirtualTester)
    {
      OnTesterCalled = true;
  
      // MQL API implies some limitations for CopyTicksRange function, so ticks are collected in OnTick
      const int size = ArraySize(_ticks);
      PrintFormat("Ticks size=%d error=%d", size, GetLastError());
      if(size <= 0) return 0;
      
      if(settings.isVoid() || !InternalOptimization) // fallback to a single virtual test without PSO
      {
        VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT));
        Print(VIRTUAL::ToString(INT_MAX));
        Print("Trades: ", VIRTUAL::VirtualOrdersHistoryTotal());
        return TesterStatistics(Estimator);
      }
      
      settings.print();
      const int n = settings.size();
  
      if(PSO_Enable)
      {
        MathSrand(PSO_GroupCount + PSO_RandomSeed); // reproducable randomization
        WorkerFunctor worker(settings);
        Swarm::Stats stats;
        if(worker.test(&stats))
        {
          double output[];
          double result = worker.getSolution(output);
          if(MQLInfoInteger(MQL_OPTIMIZATION))
          {
            FrameAdd(StringFormat("PSO%d/%d", stats.done, stats.planned), PSO_GroupCount, result, output);
          }
          ArrayResize(output, n + 1);
          output[n] = result;
          ArrayPrint(output);
          return result;
        }
      }
      ...
      return 0;
    }
    return TesterStatistics(Estimator);
  }

上面的代码显示了通过“settings”对象的一组参数创建 WorkerFunctor，并使用其“test”方法启动 swarm。所获得的结果以帧的形式发送到终端，在那里它们被 OnTesterPass 接收。

OnTesterPass 处理函数与 PPSO test EA 中的处理程序类似，只是帧中接收的数据不是打印到日志中，而是打印到名为 PPSO-EA-name-date_time的 CSV 文件中。

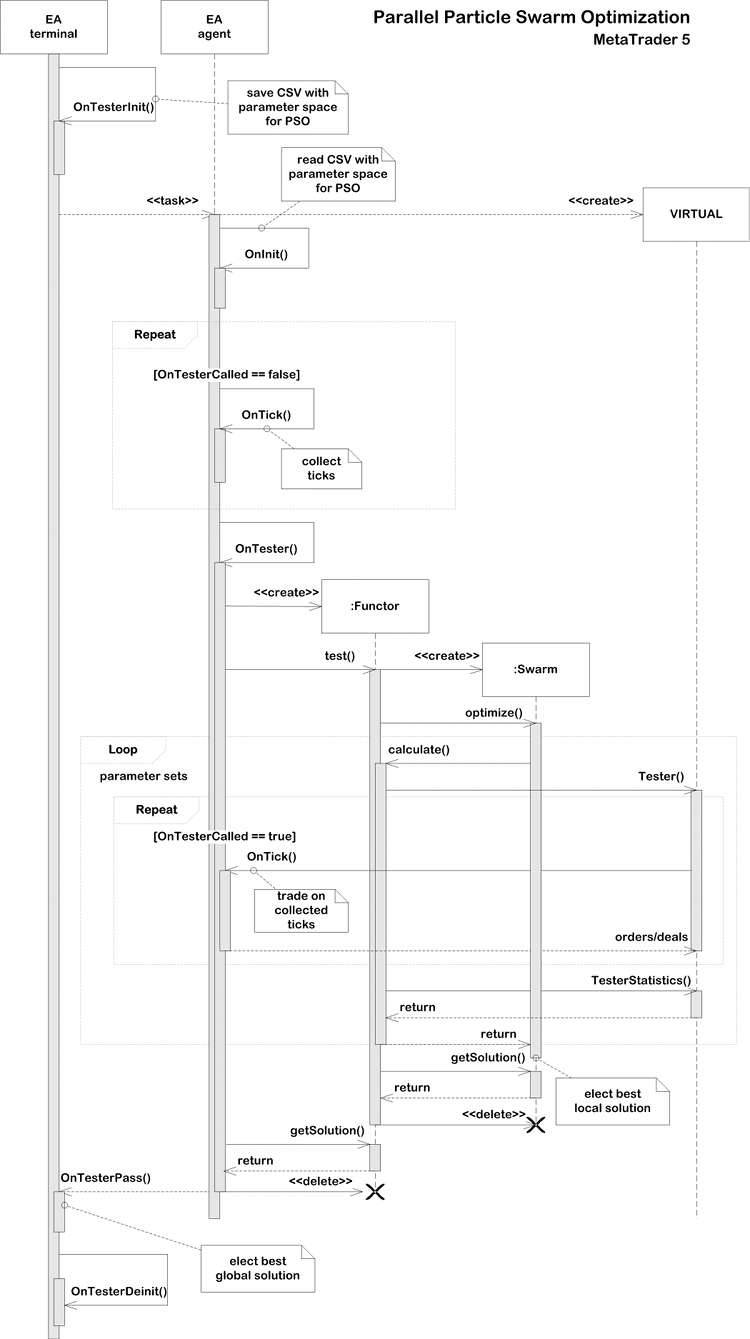
并行粒子群优化序列图

让我们最后回到交易策略。它与《计算数学表达式（第2部分）》一文中所用的方法几乎相同。然而，为了实现虚拟交易，还需要进行一些调整。以前的信号公式是基于零柱上的开盘价计算均线指数：

  input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";

现在，应该从历史条形图中读取它们（因为计算是在过程的最后，从 OnTester 执行的）。过去“current”条的编号很容易确定：虚拟库覆盖 TimeCurrent 系统函数，因此可以在 OnTick 中编写以下内容：

    const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent());

应将当前柱的编号添加到表达式的变量表中，并使用适当的名称，例如“bar”，然后可以按照以下方式重写信号公式：

  input string SignalBuy = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) > 1 + Threshold";
  input string SignalSell = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) < 1 - Threshold";

当更改变量（柱号）并使用此值计算公式时，更新版本的解析器会中间调用新的“with”方法（也在OnTick中）：

    const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent()); // NEW
    bool buy = p1.with("Bar", bar).resolve();    // WAS: bool buy = p1.resolve();
    bool sell = p2.with("Bar", bar).resolve();   // WAS: bool sell = p2.resolve();

此外，OnTick 交易代码没有变化。

然而，还需要更多的修改。

当前公式使用了设置中指定的固定的 EMA 周期数，要在表达式中转换成变量。然而，周期数应该是在优化过程变化的，这意味着使用不同的指标实例。问题是，通过 swarm 进行参数调整的虚拟优化是在测试过程中执行的，在测试过程的最后，在 OnTester 函数中执行。现在在这里创建指标句柄为时已晚。

这对于任何虚拟优化都是一个全局问题。有三个明显的解决方案：

• 完全不要使用指标；不使用任何指标的交易系统在这里有优势；
• 以一种特殊的方式计算指标，独立于EA；许多人使用这种方法，因为这是最快的方法，即使与标准指标相比，也是如此，但它需要很多工作；
• 预先为设置中的所有参数组合创建一组指标；资源密集型；可能需要限制参数范围。

最后一种方法对于逐个报价点计算信号的系统来说是有问题的。实际上，虚拟历史记录中的所有柱都已经关闭，并且已经计算了指标。换句话说，只有柱信号可用。如果我们在这样一个历史记录上运行一个系统而不控制开仓，那么与非虚拟交易相比，这将产生更少的质量更低的交易。

我们的 EA 交易是按柱来交易的，所以这不是问题。这种情况对于 MetaTrader 5 中的一些标准 EA 交易来说是典型的—有必要了解如何检测到新柱开启的事件。带有单个报价点交易量控制的方法不适用于虚拟历史记录，因为所有柱形图都已充满报价点。因此，建议通过将新柱的时间与上一个柱的时间进行比较来定义新柱。

表达式引擎已被扩展以使用第三个选项解决所描述的问题。除了单个 MA 指标函数（MAIndicatorFunc）之外，我还创建了MA Fan函数（MultiMAIndicatorFunc，请参阅 Indicators.mqh). 它们的名称必须以“M_”前缀开头，并且必须包含最小周期、周期步长和最大周期，例如：

  input string SignalBuy = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) > 1 + T";
  input string SignalSell = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) < 1 - T";

计算方法和价格类型在名称中如前所示。这里基于开放价格创建一个EMA fan，期间为9到27（包括27），步长为6。

表达式库中的另一个创新是一组变量，这些变量提供了从 TesterStatistics 访问交易统计信息的权限（参见 TesterStats.mqh). 基于此集合，可以将公式输入添加到EA，这允许将目标值设置为任意表达式。当这个变量被填充时，Estimator 就被忽略。特别是，可以在“Estimator”中设置具有类似公式的“更平滑”指标，而不是STAT_PROFIT_FACTOR（未定义为零损失）：“（GROSSPROFIT-（1/（TRADES+1）））/-（GROSSLOSS-1/（TRADES+1））”。

现在，一切都准备好使用PSO方法运行虚拟交易优化。

实际测试

让我们准备一个测试器，它应该使用慢速的优化，即所有参数的完全迭代。在我们的例子中，它不会很慢，因为在每次运行中只改变组数，而EA参数的选择性迭代是由一个群在其周期内执行的。这里不能使用遗传算法，有三个原因。首先，它不能保证所有的参数组合（在我们的例子中是给定数量的组）都会被计算出来。其次，由于其特殊性，它会逐渐向产生更具吸引力结果的参数“转移”，而没有考虑到组数与其成功之间没有依赖性，因为组数只是PSO数据结构的随机化器。第三，群体的数量通常不足以使用遗传方法。

按最大自定义准则进行优化。

首先，以常规方式优化EA交易，禁用虚拟库（ExprBotPSO-standard-optimization.set文件）。为了演示的目的，用于优化的参数组合的数量很少。Fast 和 Slow 参数的变化范围为9到45，步长为6；T参数的变化范围为0到0.01，步长为0.0025。

EURUSD, H1, 范围从2020年起始，使用真实报价点。可以得到以下结果：

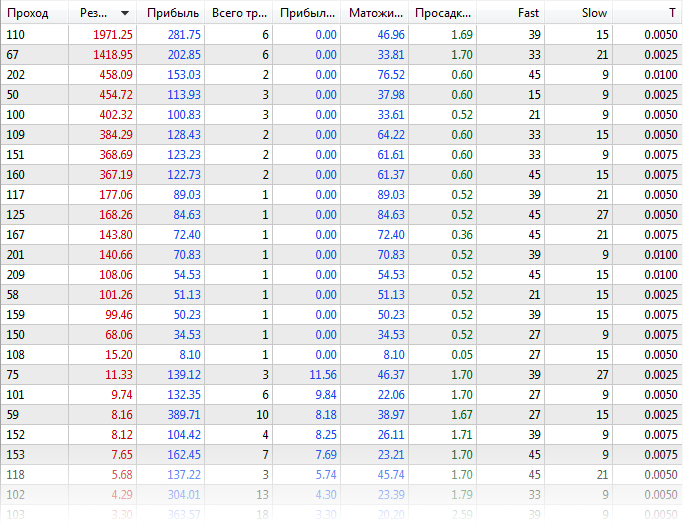
标准优化结果表格

根据日志，优化工具上的两个代理几乎工作了21分钟。

  Experts	optimization frame expert ExprBotPSO (EURUSD,H1) processing started
  Tester	Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00
  Tester	complete optimization started
  ...
  Core 2	connected
  Core 1	connected
  Core 2	authorized (agent build 2572)
  Core 1	authorized (agent build 2572)
  ...
  Tester	optimization finished, total passes 245
  Statistics	optimization done in 20 minutes 55 seconds
  Statistics	shortest pass 0:00:05.691, longest pass 0:00:23.114, average pass 0:00:10.206

现在，启用虚拟交易和PSO来优化EA交易（ExprBotPSO-virtual-pso-optimization.set)。等于4的组数是通过将 PSO_GroupCount 参数从0迭代到3来确定的。启用优化的其他操作参数将在标准优化中强制禁用，但它们将被传输到CSV文件中的代理，以便使用PSO算法进行内部虚拟优化。

同样，使用真实报价进行模拟，尽管也可以使用生成的报价点或一分钟 OHLC 进行快速计算。这里不能使用数学计算，因为报价点是在虚拟交易的测试器中收集的。

可以在测试器日志中获得以下信息：

  Tester	input parameter 'Fast' set to: enable=false, value=9, start=9, step=6, stop=45
  Tester	input parameter 'Slow' set to: enable=false, value=21, start=9, step=6, stop=45
  Tester	input parameter 'T' set to: enable=false, value=0, start=0, step=0.0025, stop=0.01
  Experts	optimization frame expert ExprBotPSO (EURUSD,H1) processing started
  Tester	Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00
  Tester	complete optimization started
  ...
  Core 1	connected
  Core 2	connected
  Core 2	authorized (agent build 2572)
  Core 1	authorized (agent build 2572)
  ...
  Tester	optimization finished, total passes 4
  Statistics	optimization done in 4 minutes 00 seconds
  Statistics	shortest pass 0:01:27.723, longest pass 0:02:24.841, average pass 0:01:56.597
  Statistics	4 frames (784 bytes total, 196 bytes per frame) received

每一个“过程”现在都是一个虚拟优化组，所以它变得更长了。但它们的总数减少了，总时间也大大减少了——只有4分钟。

来自帧的消息在日志中接收（它们显示每组的最佳读数）。不过，真实交易和虚拟交易的结果略有不同。

  22:22:52.261	ExprBotPSO (EURUSD,H1)	2 tmp-files deleted
  22:25:07.981	ExprBotPSO (EURUSD,H1)	0 PSO75/1500 0 1974.400000000025
  22:25:23.348	ExprBotPSO (EURUSD,H1)	2 PSO84/1500 2 402.6000000000062
  22:26:51.165	ExprBotPSO (EURUSD,H1)	3 PSO70/1500 3 455.000000000003
  22:26:52.451	ExprBotPSO (EURUSD,H1)	1 PSO79/1500 1 458.3000000000047
  22:26:52.466	ExprBotPSO (EURUSD,H1)	Solution: 1974.400000000025
  22:26:52.466	ExprBotPSO (EURUSD,H1)	39.00000 15.00000  0.00500

结果将不完全匹配（即使我们有一个逐点无指标的策略），因为测试器有特定的操作特性，不能在MQL库中完全重复。以下是其中的一些：

• 接近市场价格的限价订单可能通过不同的方式触发
• 保证金未计算或计算不太准确
• 佣金不会自动计算（MQL API限制），但可以通过其他输入参数进行编程
• 在净额结算模式下，订单和交易的账户处理可能有所不同
• 只支持当前交易品种

有关 Virtual 库的更多信息，请参阅相关文档和讨论。

为了调试和理解 swarm 操作，测试 EA 在一个正常的测试运行中支持一个核心上的虚拟优化模式。ExprBotPSO-virtual-internal-optimization-single-pass.set 文件是一个设置的实例，在后面的附件中。不要忘记在测试器中禁用优化。

中间结果详细记录在测试日志中。在每个循环中，每个粒子的目标函数的位置和值都由给定的 PSO_Cycles 输出。如果粒子命中已检查过的坐标，则跳过计算。

  Ticks size=15060113 error=0
           [,0]     [,1]     [,2]     [,3]
  [0,] "Fast"   "9"      "6"      "45"    
  [1,] "Slow"   "9"      "6"      "45"    
  [2,] "T"      "0"      "0.0025" "0.01"  
  PSO[3] created: 15/3
  PSO Processing...
  Fast:9.0, Slow:33.0, T:0.0025, 1.31285
  Fast:21.0, Slow:21.0, T:0.0025, -1.0
  Fast:15.0, Slow:33.0, T:0.0075, -1.0
  Fast:27.0, Slow:39.0, T:0.0025, 0.07673
  Fast:9.0, Slow:9.0, T:0.005, -1.0
  Fast:33.0, Slow:21.0, T:0.01, -1.0
  Fast:39.0, Slow:45.0, T:0.0025, -1.0
  Fast:15.0, Slow:15.0, T:0.0025, -1.0
  Fast:33.0, Slow:21.0, T:0.0, 0.32895
  Fast:33.0, Slow:39.0, T:0.0075, -1.0
  Fast:33.0, Slow:15.0, T:0.005, 384.5
  Fast:15.0, Slow:27.0, T:0.0, 2.44486
  Fast:39.0, Slow:27.0, T:0.0025, 11.41199
  Fast:9.0, Slow:15.0, T:0.0, 1.08838
  Fast:33.0, Slow:27.0, T:0.0075, -1.0
  Cycle 0 done, skipped 0 of 15 / 384.5000000000009
  ...
  Fast:45.0, Slow:9.0, T:0.0025, 0.86209
  Fast:21.0, Slow:15.0, T:0.005, -1.0
  Cycle 15 done, skipped 13 of 15 / 402.6000000000062
  Fast:21.0, Slow:15.0, T:0.0025, 101.4
  Cycle 16 done, skipped 14 of 15 / 402.6000000000062
  Fast:27.0, Slow:15.0, T:0.0025, 8.18754
  Fast:39.0, Slow:15.0, T:0.005, 1974.40002
  Cycle 17 done, skipped 13 of 15 / 1974.400000000025
  Fast:45.0, Slow:9.0, T:0.005, 1.00344
  Cycle 18 done, skipped 14 of 15 / 1974.400000000025
  Cycle 19 done, skipped 15 of 15 / 1974.400000000025
  PSO Finished 89 of 1500 planned calculations: true
    39.00000   15.00000    0.00500 1974.40000
  final balance 10000.00 USD
  OnTester result 1974.400000000025

由于优化空间小，被19个循环完全覆盖。当然，对于具有数百万个组合的实际问题，情况会有所不同。在这样的问题中，找到 PSO_Cycles、PSO_SwarmSize 和 PSO_GroupCount 的正确组合是非常重要的。

不要忘了，对于PSO，每个 PSO_GroupCount 的一个测试通过在内部执行高达 PSO_Cycles * PSO_SwarmSize 个单个虚拟的测试，这就是为什么进度指示会明显慢于通常的原因。

许多交易者试图通过连续多次运行内置的遗传优化来获得最佳结果。这将收集由于随机初始化而产生的各种测试，并且可以在多次运行后找到进度。在 PSO 的例子中，PSO_GroupCount 与多次运行遗传算法类似。单次运行的次数，在遗传算法上可以达到10000次，应该在 PSO 中分布在 PSO_Cycles * PSO_SwarmSize 乘积的两个分量之间，例如100*100。PSO_Cycles 类似于遗传算法上的世代，PSO_SwarmSize 是群体的大小。

MQL5 API EA 交易的虚拟化

到目前为止，我们已经研究了一个使用 MQL4 交易 API 编写的 EA 交易示例。这与 Virtual 库实现细节有关。但是，我想实现功能将 PSO 用于带有“新”MQL5 API 函数的 EA。为此，我开发了一个实验性的中间层，用于将 MQL5 API 调用重定向到 MQL4 API。它就是 MT5Bridge.mqh，需要 Virtual 库和/或 MT4Orders 才能运行。

  #include <fxsaber/Virtual/Virtual.mqh>
  #include <MT5Bridge.mqh>
  
  #include <Expert\Expert.mqh>
  #include <Expert\Signal\SignalMA.mqh>
  #include <Expert\Trailing\TrailingParabolicSAR.mqh>
  #include <Expert\Money\MoneySizeOptimized.mqh>
  ...

在代码开头添加 Virtual 和 MT5Bridge 之后，在其他 #include 之前，通过重新定义的“bridge”函数调用 MQL5 API 函数，从中调用“Virtual”的 MQL4 API 函数。这样，就可以虚拟化地测试和优化 EA 交易。特别是，现在可以像上面的 ExprBotPSO 示例一样运行 PSO 优化。这需要为测试人员编写（部分复制）functor 和处理程序。但是，资源和时间最密集的过程涉及指标信号对可变参数的适应。

MT5Bridge.mqh 因为它的功能没有经过广泛的测试，所以处于实验状态。这是一个概念研究的证明。您可以使用源代码进行调试和 bug 修复。

结论

我们探讨了粒子群优化算法，并在 MQL 中实现了它，支持使用测试代理的多线程处理。与使用内置的遗传优化相比，开放 PSO 设置的可用性允许在调节过程中具有更大的灵活性。除了输入参数中提供的设置外，尝试其他可调整的系数也是有意义的，我们使用这些系数作为默认值的“优化”方法的参数：inertia（惯性, 默认值 0.8）、selfBoost（自增强，默认值 0.4）和 groupBoost （组增强，默认值 0.4）。这将使算法更加灵活，但将使特定任务的设置选择更加困难。下面附带的 PSO 库可以在数学计算模式下使用（如果您有自己的虚拟报价、指标和交易机制），也可以在报价柱形模式下使用，使用第三方现成的交易模拟类，如 Virtual。