前两篇文章给大家聊了聊单因子的一些测试工具，那么有了工具我们就可以运用一下，实际的来测试一些因子，分析一下我们通过工具得出的结果是怎么样的。 本文思路主要参考《华泰金工多因子模型》以及《光大多因子系列报告》 多因子模型本质上是将对N只股票的收益-风险预测转变成对K个因子的收益-风险预测，将估算个股收益率的协方差矩阵转化为估算因子收益率协方差矩阵，极大地降低了预测工作量，提高了准确度。 多因子模型主要的有三种：

1. 宏观因子模型：使用宏观经济数据序列，如通胀率，利率等作为指标，反应股票市场和外部经济之间的关联性，并据此做出预测。

2. 基本面因子模型：使用可观察到的股票自身的基本属性，如估值水平、成长性、换手率等等，作为股票市场收益率变动的主要解释变量，其中一般归纳为基本面类、估值类、市场类。

3. 统计因子模型：从股票收益率的协方差矩阵中提取统计因子，作为股票市场收益率变动的主要解释变量，常见的统计分析方法有主成分分析法、最大似然分析和预期最大化分析等。

这其中效果较好的是基本面模型，在实际应用中，应注意基本面指标与收益率之间的经济逻辑是否与模型结果一致，以做出正确的判断。

本文通过几个基本面的因子，来阐述该方法的流程和其中的一些细节处理。 方法论：

首先是因子： 价值因子：
EP:净利润（TTM,过去12个月）/总市值
BP:净资产/总市值
SP:营业收入/总市值
NCFP:净现金流/总市值
OCFP:经营性现金流/总市值

财务质量因子：
roe_ttm  ：净资产收益率
roa_ttm  ：资产收益率
grossprofitmargin_ttm ：毛利率
profit_margin :扣非后利润率
operationcashflowratio：经营性现金流/净利润
assetturnover ： 资产周转率

成长因子： sales_growth：营收增长率
net_profit_growth：净利润增长率同比

动量因子：
return_1m  ：近n月收益率
return_3m
return_6m
return_12m
wgt_return_1m  ：近n月以日换手率作为权重求得每日收益率的算数平均值
wgt_return_3m
wgt_return_6m

取其中的一个因子数据来看一看标准化的效果： 处理前：

去极值后：

标准化处理（z-score）后：

取其中一个因子做一下t值和IC值的分析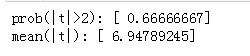：可以看出该因子显著性还不错。该因子对收益率影响基本为正向。

多重共线性的检验和消除：
计算各因子暴露之间的相关系数，对于相关系数较高的因子，可做以下处理：
1.根据有效性排序（IC,t），选取最有效因子保留 2.等权重*新因子，即将相关的因子都赋予等权重，假设有n个相关因子，则每个权重1/n，加和之后再做标准化处理。 3.历史收益率权重*新因子，方法类似2，权重变为历史收益率。 通常具有很高相关性的因子都是经济意义上较为相近和有联系的因子，我们可以做一些去除处理。

异方差检验和消除：

• 在回归中为了保证回归参数估计量有良好的统计性质，经典线性回归中有一个重要的假设是:随机误差项满足同方差性。 若不满足同方差性，会使得回归标准差的估计不再是无偏估计，从而使得OLS估计量不再有效，t统计量和F统计量不服从相应分布，故无法进行假设检验和区间估计。 通常经济数据一般都很难满足同方差的条件。
  我们可以使用White检验法进行检验： 1.回归得到OLS的残差 2.用残差项和自变量再次进行回归，即检查残差项是否与自变量有关系。 3.构造LM统计量或F统计量，看第二次回归的整体系数是否显著不为0，如果显著，则拒绝原假设（残差项同方差），即原序列有异方差性。

消除异方差的方法我们在上一篇（《全面了解多因子系列入门（二）》）中已经做了详细介绍（GLS）。

完成了这些工作之后我们就可以进行因子收益的回归分析了，同样是使用到多元线性回归，估计每一期的因子收益（这里的因子收益即以因子暴露作为自变量，股票收益作为因变量，回归得到的系数，描述了该因子对股票收益的贡献）。
我们使用增加行业哑变量的回归，能够剔除不同行业之间差异的影响（或者在之前处理数据时进行行业中性化）

做了这么多工作，其实我们想要做的事情和所有的投资者想做的事情一样，那就是预测下一期的因子收益率（这样我们才能“未卜先知”选择那些因子表现好的股票嘛）
那么估计因子预期收益也有一系列的方法： 1.历史均值法：简单地使用前N期的因子历史收益率均值作为下一期的因子预期收益率（这不是假设未来永远都是历史的中庸水平吗？感觉好像没有卵用）
2.指数加权移动平均法（EWMA）：该方法是将历史对未来的影响赋予不同的权重，按照我们直观的理解，越近的事件对下一期影响应该越大，越远的影响应该会逐渐消失。
$r_{t+1}=\lambda *r_{t}+(1-\lambda )*r_{t-1}$
通过不断迭代该式子以得到t+1时刻的因子收益率。 3.时间序列类模型：
AR（p）  、ARMA（p,q）等等做预测。

而对股票的收益预测时，则同样使用到了多因子的回归模型预测，带入t+1时刻的因子收益和t时刻的因子暴露（研报的理解是在短时期内因子暴露不会产生较大的风格性变化，故可以使用本期因子暴露作为下一期因子暴露的预测），这样就能得到股票的收益预测了。
进一步的，如果要构建策略的话，通过滚动的计算，在每一个调仓日获得下一期股票收益的预测，买入预期高收益率的组合，卖空负收益率的组合。读者可以自行尝试后面的工作。

import pandas as pdimport numpy as npimport datetimeimport timefrom math import log,expimport matplotlib.pyplot as pltimport matplotlib.mlab as mlabimport statsmodels.api as smimport numpy as np  np.set_pri*ptions(threshold=np.inf)

index = '000002.XSHG'#A股benchmark = '000300.XSHG'#沪深300#benchmark = '000016.XSHG'#上证50#benchmark = '000010.XSHG' #上证180

#过滤停牌 and ST股票def filterOfPauseAndST(stockList,startDate,endDate):import numpy as npunsuspendStock = []crew = get_price(stocklist, start_date=startDate, end_date=endDate, fields=['paused'])crew = crew.paused.Tcrew.rename(columns={crew.columns[0]:'paused'}, inplace=True)crew.dropna()pack = get_extras('is_st', stocklist, start_date=startDate, end_date=endDate, df=True)pack = pack.Tpack.rename(columns={pack.columns[0]:'is_st'}, inplace=True)unsuspended = crew[crew['paused']==0].indexunst = pack[pack['is_st']==False].indexfor stock in stockList:if (stock in unsuspended) and (stock in unst) :unsuspendStock.append(stock)return unsuspendStock

def DumVarM(stocklist,industry_index,date=None): a = map(get_industry_stocks,industry_index,[date]*len(industry_index))mix=[]for i in range(len(stocklist)):mix.append(map(lambda x: u[i] in x,a ))arr = mat(mix).astype('float64')return arr

def get_cap_factor(stocklist,date):q = query(valuation.market_cap).filter(valuation.code.in_(stocklist))#总市值版本#q = query(valuation.circulating_market_cap).filter(valuation.code.in_(stocklist)) #流通市值版本df = get_fundamentals(q,date)caplist = list(df['market_cap'].values)return caplist

#行业市值中性化#因子值对行业哑变量和市值对数进行回归取残差作为中性化后因子值def neutralization(stocks,factor,date):dumX = DumVarM(stocks,industry_index,date)capX = np.matrix(np.log(get_cap_factor(u,endDate))).TX_reg = np.column_stack((dumX,capX))model = sm.OLS(factor,X_reg).fit()res = model.residreturn res#返回的是一个（n，）的array，需要自行转化为列向量

#MAD去极值，Z-Score标准化def standarize(factorlist):#中位数去极值copy1 = factorlist[:]sort1 = sorted(copy1)if len(sort1)%2 == 0:midd = (sort1[len(sort1)/2]+sort1[len(sort1)/2-1])/2else:midd = sort1[len(sort1)/2]a = [abs(x-midd) for x in copy1]sort2 = sorted(a)
   if len(sort2)%2 == 0:midd1 = (sort2[len(sort2)/2]+sort2[len(sort2)/2-1])/2else:midd1 = sort2[len(sort2)/2-1]for i,x in enumerate(copy1):if x>(midd+5*midd1):copy1[i] = midd+5*midd1elif x<midd-5*midd1:copy1[i] = midd-5*midd1return copy1

def z_score(factorlist):return map(lambda x:(x-np.mean(factorlist))/np.std(factorlist),factorlist)

# 输入的stocks可以是单只股票或者股票列表# pointDate为计算收益率的当天# n为前n天收益率# 动量因子：return_1m,return_3m,return_6m,return_12m# n 取 30 90 180 360def calRN(stocks,pointDate,n):pastDate = pointDate - datetime.timedelta(days=n)price = get_price(stocks,start_date=pastDate,end_date=pointDate,fields='close')p = price.close.T.valuesret = p[:,-1]/p[:,0]-1ret = (ret+1)**(12/(n/30))-1ret = list(ret)return ret

def calWgt(stocks,pointDate,n):#这里多取前一天，因为求每日收益率第一行是nanpastDate = pointDate - datetime.timedelta(days=n+2)price = get_price(stocks,start_date=pastDate,end_date=pointDate,fields='close')a = price.closeb = price.close.shift(1)ret = a/b-1retlist = ret.dropna().T.valuesretlist = retlist*365#由于聚宽数据结构的原因fundamentals一次只能取一天的数据，这里只能用循环，速度较慢date = pointDateq = query(  valuation.turnover_ratio ).filter(valuation.code.in_(stocks))temp = []for i in range(n+1):flag = get_price(stocks,start_date=datetime.datetime.strftime(date,"%Y-%m-%d"),end_date=datetime.datetime.strftime(date,"%Y-%m-%d"),fields='close')if len(flag.close)!=0:temp.append(get_fundamentals(q,date).values)else:passdate = date - datetime.timedelta(days=1)#temp是所有换手率的原始数据，其中每个元素是30天中一天的1057只股票换手率的array#total分别计算了1057只股票的过去一个月总换手率total=[]sums=0for j in range(len(stocks)):for i in range(len(temp)):sums = sums+temp[i][j][0]+0.000000000000000000000000000000000001#防止有的总换手率为0，做分母时会出现nan值total.append(sums)sums=0#权重矩阵：#行为股票，1057只，列为天数，0为当前天，29为30天前#其中是换手率权重#如 weight[35,10]代表u中第36只股票在11天前换手率占上月换手率的比重weight=mat(zeros((len(stocks),len(temp))))for j in range(len(stocks)):for i in range(len(temp)):weight[j,i]=temp[i][j][0]/total[j]
   wgt = []rev = 0for i in range(len(stocks)):for j in range(len(temp)):rev = rev + weight[i,j]*retlist[i][j]wgt.append(rev)rev=0
   return wgt

def calExpWgt(stocks,pointDate,n):#这里多取前一天，因为求每日收益率第一行是nanpastDate = pointDate - datetime.timedelta(days=n+2)price = get_price(stocks,start_date=pastDate,end_date=pointDate,fields='close')a = price.closeb = price.close.shift(1)ret = a/b-1retlist = ret.dropna().T.valuesretlist = retlist*365date = pointDateq = query(  valuation.turnover_ratio ).filter(valuation.code.in_(stocks))temp = []xi=[]zjbl=[]for i in range(n+1):flag = get_price(stocks,start_date=datetime.datetime.strftime(date,"%Y-%m-%d"),end_date=datetime.datetime.strftime(date,"%Y-%m-%d"),fields='close')if len(flag.close)!=0:temp.append(get_fundamentals(q,date).values)mid = (pointDate-date).daysxi.append(mid)zjbl.append(exp(-mid*4/(n/30)))else:passdate = date - datetime.timedelta(days=1)#temp是所有换手率的原始数据，其中每个元素是30天中一天的1057只股票换手率的array#total分别计算了1057只股票的过去一个月总换手率total=[]sums=0for j in range(len(stocks)):for i in range(len(temp)):sums = sums+temp[i][j][0]+0.000000000000000000000000000000000001#防止有的总换手率为0，做分母时会出现nan值total.append(sums)sums=0
        
        #权重矩阵：#行为股票，1057只，列为天数，0为当前天，29为30天前#其中是换手率权重#如 weight[35,10]代表u中第36只股票在11天前换手率占上月换手率的比重weight=mat(zeros((len(stocks),len(temp))))for j in range(len(stocks)):for i in range(len(temp)):weight[j,i]=(temp[i][j][0]/total[j])*zjbl[i]
   expWgt = []rev = 0for i in range(len(stocks)):for j in range(len(temp)):rev = rev + weight[i,j]*retlist[i][j]expWgt.append(rev)rev=0
   return expWgt

def figureAnalysis(data):# figure analysis#kernal densitykde = mlab.GaussianKDE(data)x2 = np.linspace(min(data),max(data), 1000)line2 = plt.plot(x2,kde(x2), 'y', linewidth = 2,label="kernal density")n, bins, patches = plt.hist(data,100,normed=1, facecolor='blue', alpha=0.5)#直方图函数，x为x轴的值，normed=1表示为概率密度，即和为一，蓝色方块，色深参数0.5.返回n个概率，直方块左边线的x值，及各个方块对象y = mlab.normpdf(bins, mean(data),std(data))plt.plot(bins, y, 'r',label="normal distribution") #绘制y的曲线plt.xlabel('value') #绘制x轴plt.ylabel('Probability') #绘制y轴plt.title(r'fit figure')#中文标题 u'xxx'plt.legend(loc='upper left')

industry_index = ['801010','801020','801030','801040','801050','801080','801110','801120','801130','801140','801150','801160','801170','801180','801200','801210','801230','801710','801720','801730','801740','801750','801760','801770','801780','801790','801880','801890']

#startDate = datetime.datetime(2006,1,1,9,30)startDate = datetime.datetime(2016,12,1,9,30)endDate = datetime.datetime(2018,3,1,9,30)#pointDate = datetime.datetime(2017,12,1,9,30)stocklist = get_index_stocks(index)u = filterOfPauseAndST(stocklist,startDate,endDate)

价值因子：
EP:净利润（TTM,过去12个月）/总市值
BP:净资产/总市值
SP:营业收入/总市值
NCFP:净现金流/总市值
OCFP:经营性现金流/总市值

财务质量因子：
roe_ttm  ：净资产收益率
roa_ttm  ：资产收益率
grossprofitmargin_ttm ：毛利率
profit_margin :扣非后利润率
operationcashflowratio：经营性现金流/净利润
assetturnover ： 资产周转率

成长因子： sales_growth：营收增长率
net_profit_growth：净利润增长率同比

动量因子：
return_1m  ：近n月收益率
return_3m
return_6m
return_12m
wgt_return_1m  ：近n月以日换手率作为权重求得每日收益率的算数平均值
wgt_return_3m
wgt_return_6m

#价值因子计算q_VF = query(valuation.code, valuation.pe_ratio, valuation.pb_ratio, valuation.ps_ratio, valuation.pcf_ratio).filter(valuation.code.in_(u))df = get_fundamentals(q_VF,endDate).set_index('code')EPfactor = 1/df['pe_ratio']BPfactor = 1/df['pb_ratio']SPfactor = 1/df['ps_ratio']NCFPfactor = 1/df['pcf_ratio']

#财务因子计算q_FQ = query(valuation.code,indicator.roe,indicator.roa,indicator.gross_profit_margin,indicator.net_profit_margin,indicator.adjusted_profit_to_profit,indicator.ocf_to_operating_profit,income.total_operating_revenue,balance.total_assets).filter(valuation.code.in_(u))df1 = get_fundamentals(q_FQ,endDate).set_index('code')roefactor = df1['roe']roafactor = df1['roa']gpmfactor = df1['gross_profit_margin']pmfactor = df1['adjusted_profit_to_profit']*df1['net_profit_margin']atfactor = df1['total_operating_revenue']/df1['total_assets']oopfactor = df1['ocf_to_operating_profit']

#成长因子计算q_GF = query(valuation.code,indicator.inc_revenue_year_on_year,indicator.inc_net_profit_year_on_year).filter(valuation.code.in_(u))df2 = get_fundamentals(q_GF,endDate).set_index('code')incGfactor = df2['inc_revenue_year_on_year']netGfactor = df2['inc_net_profit_year_on_year']

#动量因子计算return_1m = calRN(u,endDate,30)return_3m = calRN(u,endDate,90)return_6m = calRN(u,endDate,180)return_12m = calRN(u,endDate,360)wgt_return_1m = calWgt(u,endDate,30)wgt_return_3m = calWgt(u,endDate,90)wgt_return_6m = calWgt(u,endDate,180)

plot(wgt_return_6m)

[<matplotlib.lines.Line2D at 0x7f37c8e3c290>]

plot(standarize(wgt_return_6m))

[<matplotlib.lines.Line2D at 0x7f37d4b0bed0>]

figureAnalysis(wgt_return_3m)

figureAnalysis(standarize(wgt_return_3m))

figureAnalysis(z_score(wgt_return_3m))

#tt_stat={}timestamp = pd.date_range(startDate,endDate,freq='M')for date in timestamp:logret = np.log(get_price(u,end_date=date,fields='close',count=2).close.T.iloc[:,1]/get_price(u,end_date=date,fields='close',count=2).close.T.iloc[:,0])df = get_fundamentals(q_VF,date).set_index('code')BPfactor = 1/df['pb_ratio']model = sm.OLS(logret,BPfactor).fit()t_value = model.params/model.bset_stat[date] = t_valuepd.Series(t_stat)

2016-12-31 09:30:00     pb_ratio   -2.714229
dtype: float64
2017-01-31 09:30:00     pb_ratio   -7.700975
dtype: float64
2017-02-28 09:30:00     pb_ratio   -9.109835
dtype: float64
2017-03-31 09:30:00     pb_ratio   -1.614685
dtype: float64
2017-04-30 09:30:00     pb_ratio   -7.199039
dtype: float64
2017-05-31 09:30:00     pb_ratio   -0.381703
dtype: float64
2017-06-30 09:30:00     pb_ratio   -1.677513
dtype: float64
2017-07-31 09:30:00    pb_ratio   -12.645502
dtype: float64
2017-08-31 09:30:00     pb_ratio   -1.993199
dtype: float64
2017-09-30 09:30:00      pb_ratio   -9.85773
dtype: float64
2017-10-31 09:30:00     pb_ratio   -8.791854
dtype: float64
2017-11-30 09:30:00     pb_ratio    8.902485
dtype: float64
2017-12-31 09:30:00    pb_ratio   -11.334248
dtype: float64
2018-01-31 09:30:00     pb_ratio    18.88212
dtype: float64
2018-02-28 09:30:00     pb_ratio    1.462943
dtype: float64
dtype: object

#ICdatebegan = timestamp[0]df = get_fundamentals(q_VF,datebegan).set_index('code')BPfactor = 1/df['pb_ratio']for date in timestamp:logret = np.log(get_price(u,end_date=date,fields='close',count=2).close.T.iloc[:,0]/get_price(u,end_date=date,fields='close',count=2).close.T.iloc[:,1])corr = logret.corr(BPfactor)print "IC:",corrdf = get_fundamentals(q_VF,date).set_index('code')BPfactor = 1/df['pb_ratio']

IC: -0.0906616445869
IC: -0.00245872750451
IC: -0.0607410932649
IC: 0.0182631803712
IC: 0.0118782587615
IC: -0.112650657267
IC: 0.0651148549123
IC: -0.148153908276
IC: 0.125992657127
IC: 0.106328679642
IC: 0.0778156865195
IC: 0.0406853084862
IC: 0.0590477289408
IC: -0.0753420352392
IC: 0.0334512167471