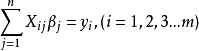基于因子模型的选股策略是股票市场量化应用最广泛的模型之一。然而很多时候,使用因子模型在实盘运行的绩效并不理想,究其原因可能是由于因子选择的偏差,市场风格轮动等。但还有一个显著的因素,就是选取因子之间可能存在高度的多重共线性,导致模型对股票价格与市场的解释能力存在很大偏误。
为了在筛选因子之初就避免陷入这样的误区。本文介绍一种VIF(方差膨胀检验)方法,来对因子之间的线性相关关系进行检验,从而帮助投资者们在可以选取到独立性更好的因子,增强因子模型的解释能力。
一、 方法介绍
所谓VIF方法,计算难度并不高。在线性回归方法里,应用最广泛的就是最小二乘法(OLS),
其中有一个检验模型解释能力的检验统计指标为R^2(样本可决系数),R^2的大小决定了解释变量对因变量的解释能力。而为了检验因子之间的线性相关关系,我们可以通过OLS对单一因子和解释因子进行回归,然后如果其R^2较小,说明此因子被其他因子解释程度较低,线性相关程度较低。
注:之所以不使用协方差计算相关性是由于协方差难以应用在多元线性相关情况下。
给出VIF计算方法:
VIF=1/(1-R^2)
从上文很容易看出,VIF越高解释变量和因变量之间线性相关性就越强。
二、 检验实践
数据来源:聚宽量化平台投资研究板块
选取因子:EPS(每股收益),ROE(净资产收益率),market_cap(市值),pb(市净
率),'net_profit_ratio','gross_income_ratio','quick_ratio','current_ratio'(后面四个因子来源于聚宽因子库)
时间窗口选取:2012.3.4—2018.7.4
回望频率:两个月
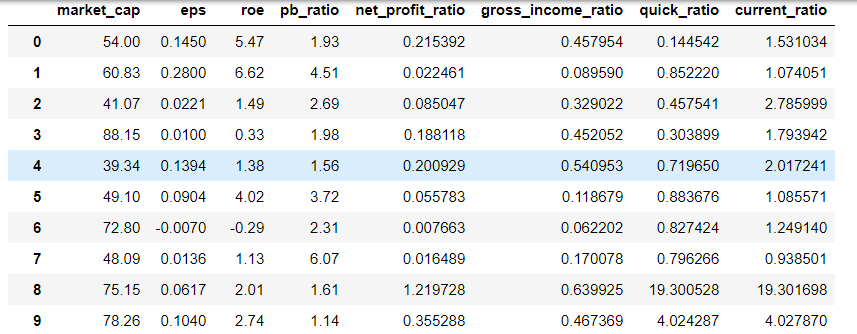
1.获取数据:(鉴于篇幅仅展示2012-03-04当日前十支股票相关因子数据)
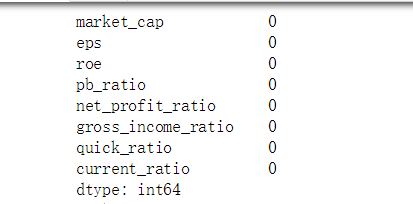
2.缺失值检验:(鉴于篇幅仅展示2013-03-04当日检验情况)
返回0代表无缺失值,返回其他数字代表缺失值数量
3.被检验两两因子间线性相关性预了解(图例,鉴于篇幅仅展示2013-03-04当日检验情况)
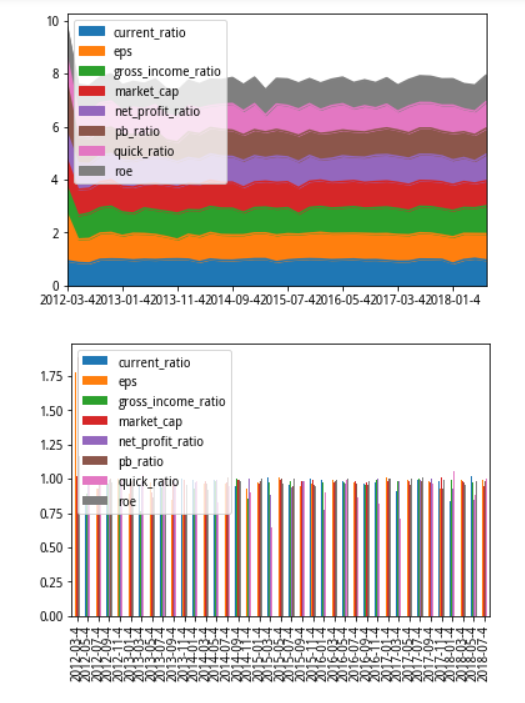
4.计算并获取每个时点下被解释因子与其余7个因子之间的回归VIF值,绘制时间序列图。
堆积图每一层上下宽幅为其颜色对应的因子取值,从中可以更明显看出不同因子VIF在同一时期的变化情况。下面的柱状
图则代表实际每个时间窗口下各个因子的VIF值
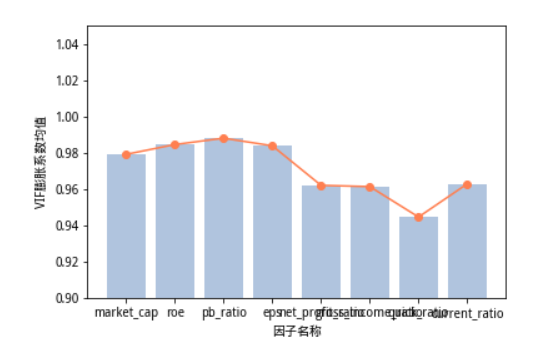
5.计算时间窗口内VIF值均值,比较大小(图例)
6.相比而言quick_ratio这一因子的VIF在窗口期平均值较低,因而这就提示了我们如果在构建因子模型时,采用其余其中
因子时可以考虑添加这一因子,增强模型的解释能力。
三、方法总结
使用VIF进行检验的方法主要为,对某一因子和其余因子进行回归,得到R^2,计算VIF,剔除因子中VIF高的因子,保留VIF较低的因子,以此类推,直到得到一个相关性较低的因子组合来增强模型的解释能力。
#基本面因子的VIF检验
#选取因子 EPS(每股收益),ROE(净资产收益率),market_cap(市值),pb(市净率)
#时间窗口选取90天
#导入必要的工具包
from jqlib.alpha191 import *
from jqdata import*
from jqfactor import get_factor_values
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split
from sklearn.linear_model import LinearRegression
import seaborn as sns
#选取测试时期
section_time_list =\
['2012-03-4','2012-05-4','2012-07-4','2012-09-4','2012-11-4',
'2013-01-4','2013-03-4','2013-05-4','2013-07-4','2013-09-4','2013-11-4',
'2014-01-4','2014-03-4','2014-05-4','2014-07-4','2014-09-4','2014-11-4',
'2015-01-4','2015-03-4','2015-05-4','2015-07-4','2015-09-4','2015-11-4',
'2016-01-4','2016-03-4','2016-05-4','2016-07-4','2016-09-4','2016-11-4',
'2017-01-4','2017-03-4','2017-05-4','2017-07-4','2017-09-4','2017-11-4',
'2018-01-4','2018-03-4','2018-05-4','2018-07-4']
#因子列表
factor_list=['market_cap','roe','pb_ratio','eps','net_profit_ratio','gross_income_ratio','quick_ratio','current_ratio']
jq_factors_list=['net_profit_ratio','gross_income_ratio','quick_ratio','current_ratio']
#获取因子数据
def get_data(date):
stock_list=get_index_stocks('000905.XSHG',date)
q=query(valuation.market_cap,
indicator.eps,
indicator.roe,
valuation.pb_ratio) .filter(valuation.code.in_(stock_list))
basic_data=get_fundamentals(q,date=date)
for jq_factor in jq_factors_list:
jq_factor_data=get_factor_values(securities=stock_list,factors=[jq_factor], count=1,end_date=date)
jq_factor_data_T=jq_factor_data[jq_factor].fillna(0).T
basic_data[jq_factor]=array(jq_factor_data_T)
return basic_data
get_data(section_time_list[0])
#缺失值检验,若返回不为0,则存在缺失值
def check_data(date):
checking_data = get_data(date)
print(checking_data[checking_data.isnull()==True].count())
for date in section_time_list:
check_data(date)
#输出时期各个因子之间相关性并绘制95%置信区间散点图(鉴于运算性能,只以2012年3月数据市值和其他个体为例,直线置信区间95%)
def plot_corr_liner(date,aim_factor):
bas_date=get_data(date)
copy_list=factor_list.copy()
copy_list.remove(aim_factor)
sns.pairplot(bas_date, x_vars=copy_list, y_vars=aim_factor, size=7, aspect=0.8,kind = 'reg')
plt.figure(figsize=(600,6.5))
plt.savefig("pairplot.jpg")
plt.show()
print(bas_date.corr())
plot_corr_liner(section_time_list[0],'market_cap')
#对因子之间进行多元线性回归来观察每个单独因子和其他多因子的线性相关性
def sqr_R_check(data,aim_factor):
#数据处理,特征分类
tset_data_y=get_data(data)[aim_factor]
copy_list=factor_list.copy()
copy_list.remove(aim_factor)
tset_data_x=tset_data[copy_factor]
X_train,X_test,Y_train,Y_test = train_test_split(tset_data_x,tset_data_y,train_size=.500)
#建立回归模型
model = LinearRegression()
model.fit(X_train,Y_train)
#R^2检测
score = model.score(X_test,Y_test)
return data,aim_factor,score
#创建数据收集字典
factor_analist_dict={}
for date in section_time_list:
factor_analist_dict[date]={}
#对每一个因子在不同时期的R^2进行数据填充
for date in section_time_list:
for factor in factor_list:
current_date,which_factor,factor_sorce=sqr_R_check(date,factor)
factor_analist_dict[current_date][which_factor]=1/(1-factor_sorce)
#输出因子在不同时期 VIF系数,并通过堆积图和直方图进行绘制
VIF_df=pd.DataFrame(factor_analist_dict)
VIF_analist=VIF_df.T
VIF_analist.plot(kind='area')
VIF_analist.plot(kind='bar')
#计算并输出因子均值并绘图
factor_mean={}
for factor in factor_list:
factor_mean[factor]=mean(VIF_analist[factor])
factor_name=[]
factor_num=[]
for key in factor_mean.keys():
factor_name.append(key)
factor_num.append(factor_mean[key])
plt.bar(range(8),factor_num,color = 'lightsteelblue')
plt.plot(range(8),factor_num,color='coral',marker = 'o')
plt.xticks(range(8),factor_name )
plt.xlabel('因子名称')
plt.ylabel("VIF膨胀系数均值")
plt.ylim((0.9, 1.05))
plt.show()