在早前的文章中,我们曾研究过操作原理,以及完全连接感知器、卷积和递归网络的方法实现。 我们利用梯度下降来训练所有网络。 根据这种方法,我们判断每个步骤的网络预测误差,并调整权重来减少误差。 然而,我们并没有完全消除每一步的误差,而只是调整权重来减少误差。 如此,我们正在尝试找到这样的权重,并沿其整体长度紧密地重复训练集。 学习率负责在每步中将误差最小化。
选择学习率有什么问题? 我们来概括与学习率选择有关的基本问题。
1. 为什么我们不能使用等于 “1”(或接近值)的比率来立即补偿误差?
在这种情况下,我们将针对最后一种情形对神经网络进行过度训练。 结果则为,忽略历史记录,仅基于最新数据做出进一步的决策。
2. 已知的较小速率允许对整个样本进行平均计算,这样会带来什么问题?
该方法的第一个问题是神经网络的训练周期。 如果步幅太小,则需要大量的步骤。 而这需要时间和资源。
该方法的第二个问题是,通往目标的道路并不总是一帆风顺的。 也许会有山谷和丘陵。 如果我们以太小的步幅移动,我们可能会被其中一个值卡住,从而错误地将其确定为全局最小值。 在这种情况下,我们将永远无法实现目标。 这可通过在权重更新公式中使用动量来部分解决此问题,但问题仍然存在。
3. 已知的较大速率允许在一定距离内进行数值平均,并避免局部最小值,这样会有什么问题?
尝试通过提高学习率来解决局部最小值问题,会引发另一个问题:采用较大的学习率通常无法将误差最小化,因为随着下一次更新权重,它们的变化将大于所需,故此我们将跳过全局最小值。 如果我们以后再次返回,情况依然类似。 结果就是,我们将在全局最低值附近徘徊。
这些都是众所周知的问题,它们经常被讨论,但我还没有找到有关学习率选择的明确建议。 每个人都建议根据经验为每个特定任务选择速率。 一些其他作者则建议在学习过程中逐渐降低速率,从而令上述风险 3 最小化。
在本文中,我提议进行一些实验,以不同学习率来训练一个神经网络,并从整体上查看此参数对神经网络训练的影响。
出于便捷起见,我们将 CNeuronBaseOCL 类中的 eta 变量设为全局变量。
double eta=0.01; #include "NeuroNet.mqh"
且
class CNeuronBaseOCL : public CObject { protected: ........ ........ //--- //const double eta;
现在,以不同学习率参数(0,1; 0,01; 0,001)创建智能交易系统的三个副本。 另外,创建第四个 EA,将初始学习率设置为 0.01,并每经过 10 个周期将其降低 10 倍。 为此,将以下代码添加到 “Train” 函数的训练循环中。
if(discount>0) discount--; else { eta*=0.1; discount=10; }
所有四个 EA 在一个终端中同时启动。 在此实验中,我采用早前 EA 测试中的参数:品种 EURUSD,时间帧 H1,连续 20 根烛条的数据输入到网络中,并用最近两年的历史记录进行训练。 训练样本约为 1.24 万根柱线。
所有 EA 均以 -1 到 1 的随机权重进行初始化(不包括零值)。
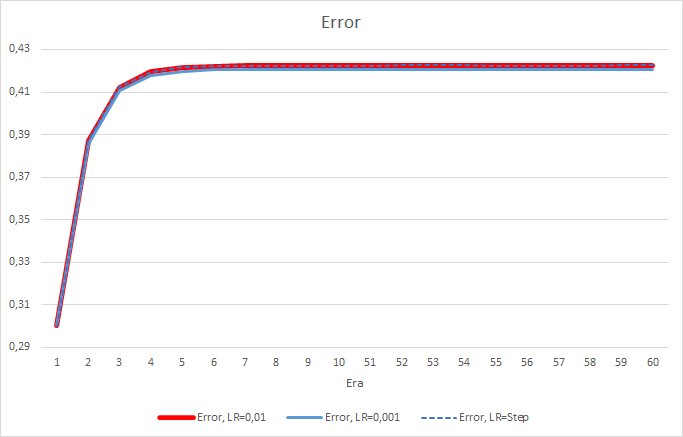
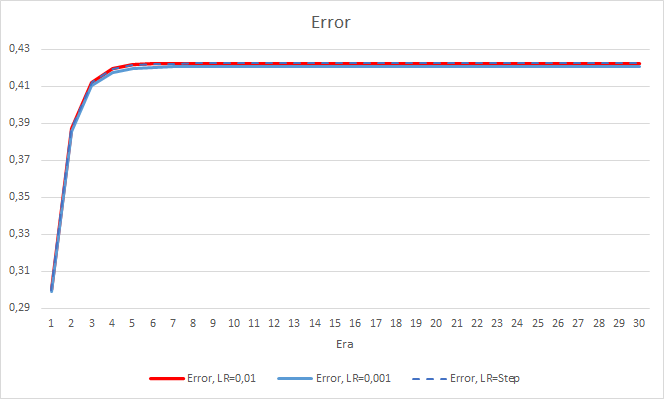
不幸的是,学习率等于 0.1 的 EA 误差接近 1,因此未在图表中显示。 以下图表显示了其他 EA 的学习动态。
5 个迭代之后,所有 EA 的误差均达到 0.42 的水平,而在其余时间内,该误差会继续波动。 学习率等于 0.001 的 EA 误差略低。 差异出现在小数点后第三位(其他两个 EA 的 0.420 对比 0.422)。
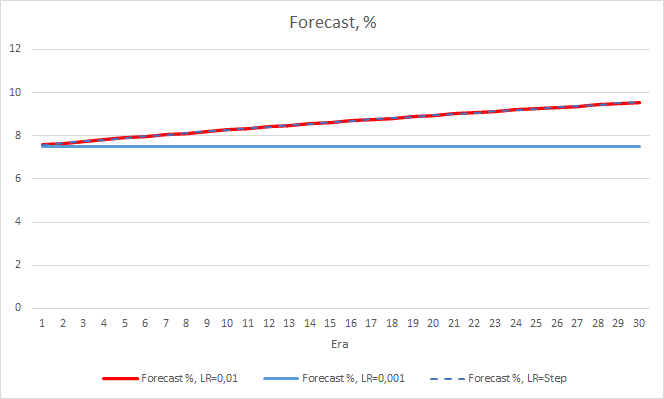
具有可变学习率的 EA 其误差轨迹遵循学习因子为 0.01 的 EA 误差曲线。 在前十个迭代中这是完全可以预期的,但是当速率降低时没有偏差。
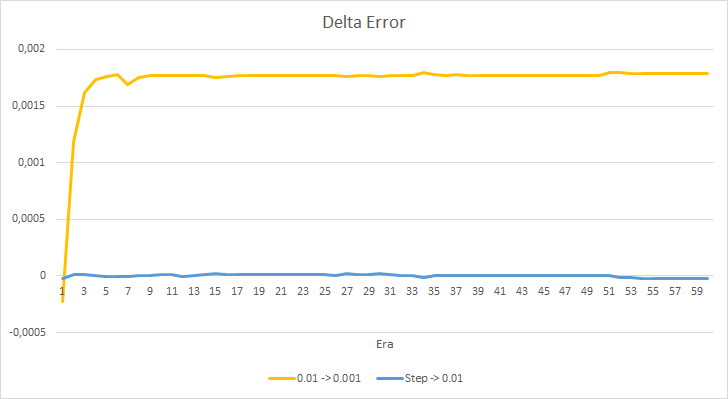
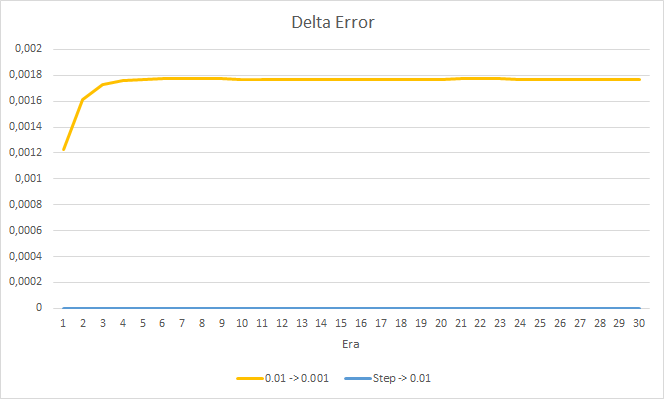
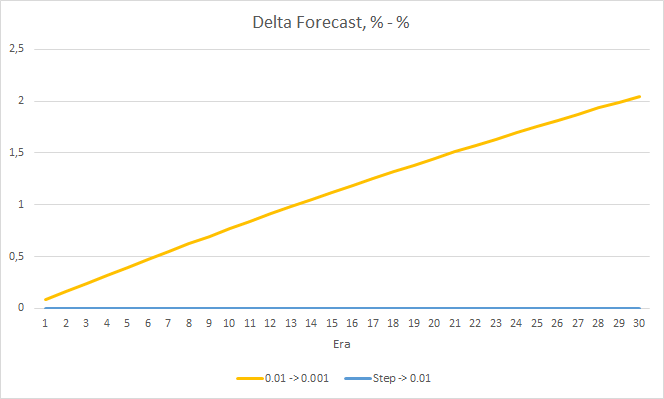
我们仔细看看上述 EA 的误差之间的区别。 几乎贯穿整个实验,恒定学习率分别为 0.01 和 0.001 的 EA 它们误差之间的差值在 0.0018 左右波动。 甚或,EA 的学习速率每 10 个迭代降低一次几乎没有影响,且速率为 0.01(等于初始学习速率)的 EA 其偏差在 0 附近波动。
所获得的误差值表明 0.1 的学习率不适用于我们的情况。 采用 0.01 及以下的学习率会产生相似的结果,误差约为 42%。
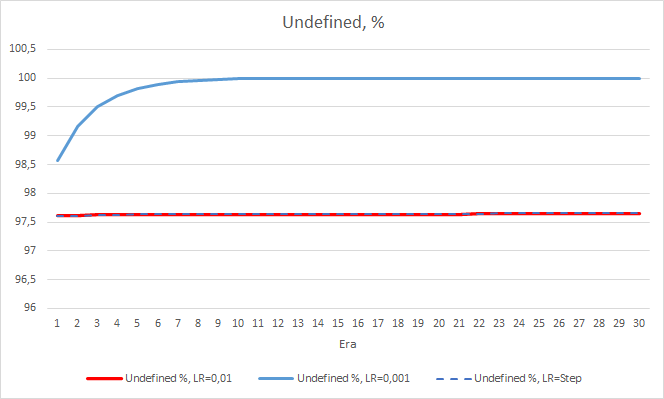
神经网络的统计误差非常明显。 这将如何影响 EA 的性能? 我们来检查漏掉的分形数量。 不幸的是,所有 EA 在实验过程中均显示不良结果:它们都错过了近 100% 的分形。 甚而,学习率为 0.01 的 EA 判断出约 2.5% 的分形,而学习率为 0.001 的 EA 则跳过了 100% 的分形。 在第 52 个迭代之后,学习率为 0.01 的 EA 表现出掠过分形的数量降低的趋势。 可变速率的 EA 并未展现出这种趋势。
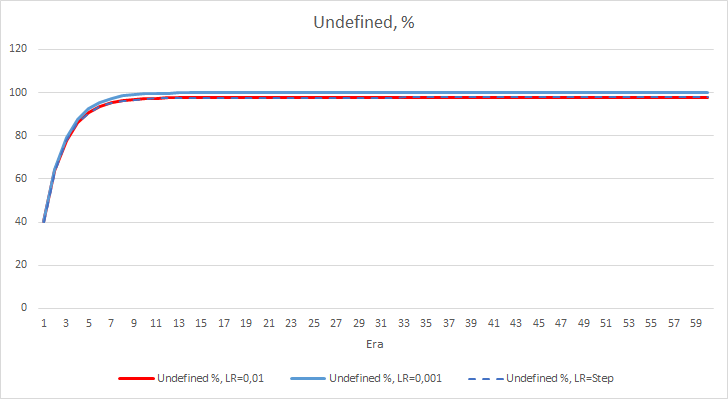
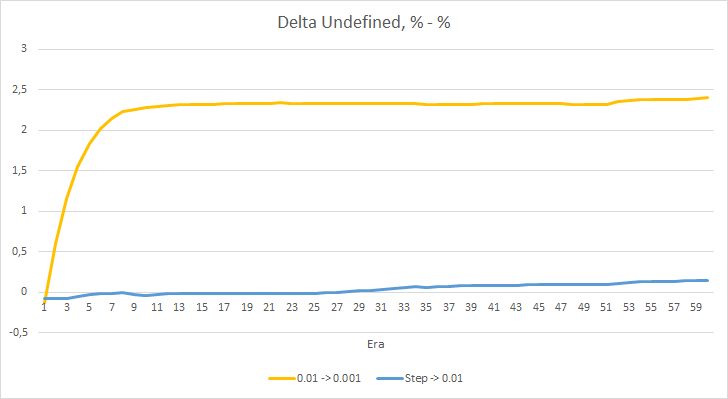
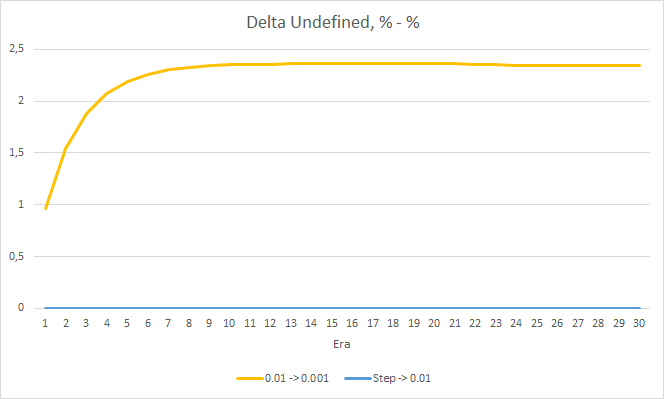
遗漏分形的百分比增量图表还显示,学习率为 0.01 时,EA 的差值逐渐增加。
我们已研究过两个神经网络性能指标,到目前为止,学习率较低的 EA 的误差较小,但会遗漏分形。 现在,我们检查第三个数值:预测分形的“命中”。
以下图表显示了学习率为 0.01 且速率动态下降的 EA 在训练中“命中”百分比的增长情况。 变化增长的速率随着学习速率的降低而降低。 学习率为 0.001 的 EA 其“命中”百分比在 0 附近卡住,这很自然,因为它错过了 100% 的分形。
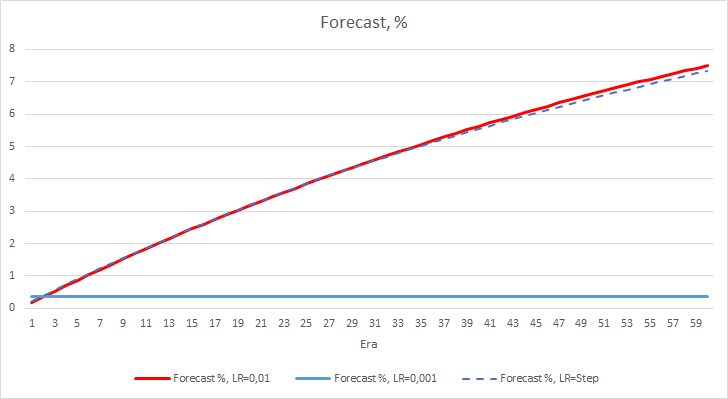
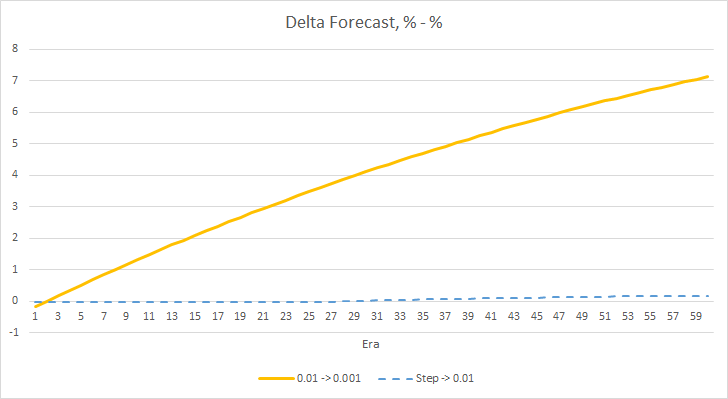
以上实验表明,最佳学习率,或在我们的问题范围内训练的神经网络,其值接近 0.01。 学习率的逐渐降低并未得到积极的结果。 如果我们把速率降低到少于 10 个迭代,速率降低的影响可能会有所不同。 也许,100 或 1000 个迭代效果会更好。 然而,这需要由实验进行验证。
在第一个实验中,神经网络权重矩阵以随机方式初始化。 并因此,所有 EA 都有不同的初始状态。 为了消除随机性对实验结果的影响,采用之前实验中学习速率等于 0.01 的 EA 的权重矩阵,将其加载到所有三个 EA 中,并继续训练额外的 30 个迭代。
新的训练过程证实了早前获得的结果。 我们看到所有三个 EA 的平均误差约为 0.42。 最低学习率(0.001)的 EA 再次得到较小的误差(相同差值 0.0018)。 学习率逐渐降低的影响实践当中等于 0。
至于漏掉分形的百分比,再次确认了较早获得的结果。 学习因子较低的 EA 在 10 个迭代内遗漏分形接近 100%,即 EA 无法识别分形。 其他两个 EA 的数值为 97.6%。 学习率逐渐降低的影响实践当中等于 0。
学习率为 0.001 的 EA 的“命中”百分比持续递增。 学习率的递减不会影响该数值。
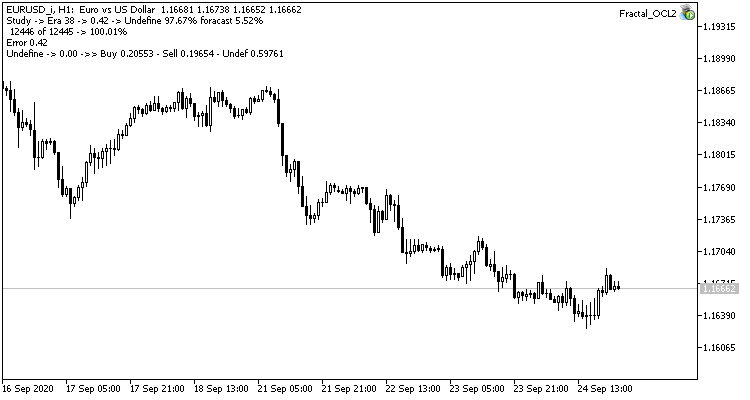
第三个实验与本文的主题略有偏离。 其思路来自前两个实验。 因此,我决定与您分享。 在观察神经网络训练的同时,我注意到不存在分形的概率在 60-70% 左右波动,且很少低于 50%。 无论买入或卖出,出现分形的可能性均约为 20% 至 30%。 这是很自然的,因为图表上的分形比趋势内的烛条少得多。 因此,我们的神经网络被过度训练,且我们获得了以上结果。 几乎 100% 的分形都遗漏了,且只能捕获罕有的分形。
为了解决这个问题,我决定稍微补偿样本的不均匀性:由于参考值中缺乏分形,因此在训练网络时我指定了 0.5 来替代 1。
TempData.Add((double)buy); TempData.Add((double)sell); TempData.Add((double)((!buy && !sell) ? 0.5 : 0));
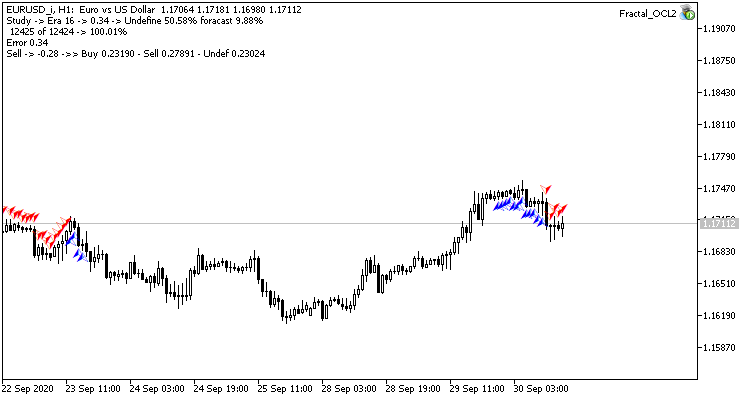
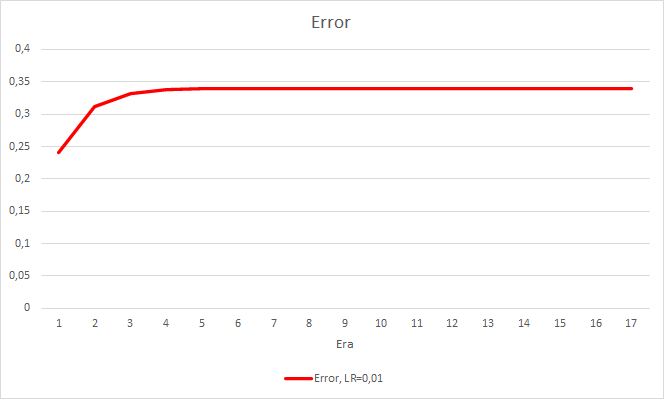
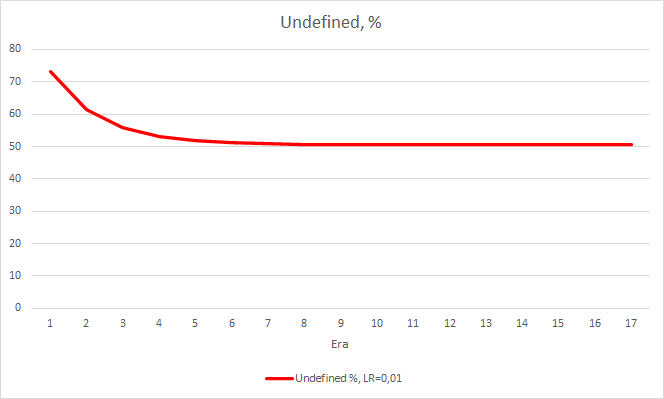
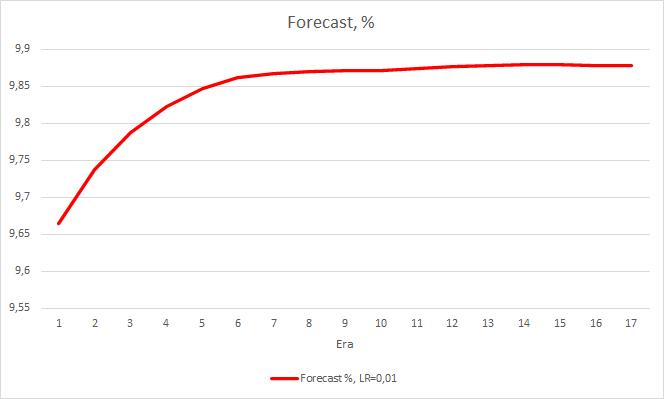
该步幅产生了良好的效果。 以 0.01 的学习率和从之前的实验获得的权重矩阵运行 智能交易系统,在 5 个训练迭代后显示出约 0.34 的稳定误差。 分形遗漏的比例下降到 51%,命中百分比则增加到 9.88%。 从图表中可以看出,EA 生成的信号会成组出现,从而显示某些特定区域。 显然,这个想法需要额外的开发和测试。 但结果表明这种方法很有前途。
我们在本文中实现了三个实验。 前两个实验已表明正确选择神经网络学习率的重要性。 学习率会影响整个神经网络训练结果。 不过,目前尚无选择学习率的明确规则。 这就是为什么您必须在实践中经由实验选择它的原因。
第三个实验表明,解决问题的非标准方法可以改善结果。 但是每种方案的应用都必须经过实验确认。
| # | 名称 | 类型 | 说明 |
|---|---|---|---|
| 1 | Fractal_OCL1.mq5 | 智能交易系统 | 利用 OpenCL 技术,且学习率 = 0.1 的含有分类神经网络(输出层中有 3 个神经元)的智能交易系统 |
| 2 | Fractal_OCL2.mq5 | 智能交易系统 | 利用 OpenCL 技术,且学习率 = 0.01 的含有分类神经网络(输出层中有 3 个神经元)的智能交易系统 |
| 3 | Fractal_OCL3.mq5 | 智能交易系统 | 利用 OpenCL 技术,且学习率 = 0.001 的含有分类神经网络(输出层中有 3 个神经元)的智能交易系统 |
| 4 | Fractal_OCL_step.mq5 | 智能交易系统 | 利用 OpenCL 技术,且学习率从 0.01 开始每 10 次迭代降低 10 倍,含有分类神经网络(输出层中有 3 个神经元)的智能交易系统 |
| 5 | NeuroNet.mqh | 类库 | 用于创建神经网络的类库 |
| 6 | NeuroNet.cl | 代码库 | OpenCL 程序代码库 |

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...
移动端课程
