根据 Merriam-Webster 定义之一,趋势是统计可检测变化随时间变化的总体走势,也是反映这种变化的统计曲线。 在数学中,趋势可以采用各种方程式来描述 — 线性、对数、多项式、等等。 实际趋势类型是根据其功能模型的选择,并按统计方法或按平滑初始时间序列而建立的。
在经济学中,趋势是经济指标的总体方向。 通常在技术分析的框架内考虑它,暗示价格走势或指数值的方向。 根据查尔斯·道(Charles Dow)的说法,上行趋势(看涨趋势)的特征是图表上的每个后续峰值均高于前一个峰值,而下行趋势(看跌趋势)则意味着随后的每个底部均应低于之前的底部(请参阅道氏理论)。 如果图表窄幅震荡,则表示横盘走势。 在看涨趋势的情况下,趋势线应连接两个或多个价格的底部(该线位于图表下方,在视觉上就像支撑并向上推升)。 在看跌趋势的情况下,趋势线应连接两个或多个价格的顶部(该线位于图表上方,在视觉上就像阻力并向下压制)。 趋势线用作支撑(对于上行趋势)和阻力线(对于下行趋势)。
然而,这不是我们感兴趣的术语,而是从中获利的能力。 上面的术语不能揭示如何在数学上将其形式化。 所有众所周知的定义听起来都比较模糊,并可用多种途径来解释。 按其本意,科学喜欢准确性。 定义应该清晰、可理解、且解释无歧义,从而采用该方法的任何人都可以重现以前的其他人采用相同方法得到的结果。</ s0>
为了继续研究趋势和横盘的概念,我们首先需要了解基本知识,即为了赚钱需要做些什么。 任何交易策略都需要预期收益大于 0。 那些精通数学的人不需要进一步的解释,但我仍然会提供它们。 简而言之,期望收益(利润的数学期望)是平均利润。 自然地,平均利润应超过 0。 如果等于 0,我们就没有利润。 如果它低于 0,那么我们会亏损。
预期收益由获利成交的概率、平均利润和平均损失构成。 方程很简单:利润概率乘以平均利润。 从所获结果中减去亏损概率乘以平均亏损。
m=(P(tp)*tp)-(P(sl)*sl),
其中
这意味着,如果获利成交的概率为 50%,而获利成交的平均大小等于亏损成交的大小,则期望值为 0,这意味着我们一无所获。 例如,获胜和亏损成交的平均大小为 $10,则 m=(50*10)-(50*10)=0。 正态分布随机变量的预期收益为 0(这是一个数学事实)。 在我以前的文章价格序列离散,随机分量和“噪音”中,我认为真实市场中增量的分布与正常情况非常相似,并且与随机漫步相似。
为了获利,我们要么增加获利成交的概率,要么增加获利成交的平均规模,并减少亏损成交的平均规模。 假设我们将获利成交的概率提高到 60%,而平均获利成交等于平均亏损成交 = $10。 然后,在完成 100 笔成交后,我们将赚取 m=(60*10)-(40*10)=$200。 如果获利成交概率保持不变,那么我们将获得稳定的利润。 与此类似,如果我们增加平均盈利成交规模,减少平均亏损成交规模,并将概率保持在 50%,我们也将获得稳定的利润。
这是许多交易者(尤其是新手)经常开始出现认知偏差的所在。 他们认为:“好吧,我简单地令获利成交的平均规模比亏损成交的平均规模大两倍,并开仓 ... 或是说,在移动平均线的交点处(此处的入场算法并不重要)。 他们下意识地希望达成结果:m=(50*20)-(50*10)=$500,但实际上,他们只能得到预期收益 m=(33,3*20)-(66,6*10)=0,或者很可能由于点差和佣金造成亏损。 我不会在本文中研究点差和佣金,因为它们在此不是重点。 其他一些交易者可能陷入相反的陷阱:他们也许决定赚取的利润是亏损的两倍,因为根据他们的观察,在这种情况下应该更频繁地触发盈利成交。 而结果呢,他们也因佣金和点差而蒙受亏损,因为事实证明,这种系统的实际预期收益为 m=(66,6*10)-(33,3*20)=0。 这z种方式,我们可以极大地增加止损,并减少盈利,从而令获利概率达到 90-99% 或更高,但所有利润最终都被亏损所抵消。 这还包括所有的马丁格尔系统,它们不会改变预期收益,因为它保持为 0,而亏损可能只是在时间上大大延迟而已。
发生这种情况是因为实际上没有找到任何可盈利的形态。 取而代之的是,交易者基于随机漫步进行交易。 随机漫步的预期收益为 0。 如果预期收益为 0,则获利成交的概率仍为 50%。 唯一改变的是比率(从现在开始,我将其称为 “50% 平衡”)。 因此,我们要么在减少成交规模的同时增加获利成交的概率,要么在增加成交规模的同时减少获利成交的概率。 我们需要以某种方式打破这个 “50% 平衡”,并超越零收益预期。 值得注意的是,开发一个亏损系统同样困难。 交易者由于佣金和有限本金而遭受亏损。
由于我们交易的价格变化以点数(最小可能的价格变化)为基础,并且利润取决于价格已覆盖了多少点数,因此我们需要远离以蜡烛/柱线表示价格的标准方式,因为它们会极大地扭曲图形,令过程难以理解。 我们继续研究仅以点数为单位显示价格走势的方法。 在本文中,我将运用我自己的指标,该指标在价格移动一定点数后构建砖形。 该指标附于文后。 不过,您也可以自由使用任何其他方法。 图例 1 示意如何构建砖形。 砖形可以是任意大小,从一个点数到无穷大(以一个点数为增量)。 如果砖形大小为 10 个点数,则在价格垂直移动 10 个点数后该砖形收盘,并形成砖形。 该砖形无论向上或向下增加 10 个点数,均可收盘。 该砖形可提供开盘价、最高价、最低价和收盘价,与蜡烛的功能相似。 一块砖形可考虑 作为一个步骤。 这在稍后将很重要。
图例 1
为了继续研究趋势概念,我们需要一些样本。 在随机漫步当中,每个后续步骤都不依赖于前一个步骤,该过程没有记忆,并且下一步骤方向变化的可能性为 50%。 但是随机漫步是基于趋势还是横盘? 我们来看一下图例 2 中的随机漫步图表。
图例 2
如果需要,我们可以在图例 2 中找到趋势和横盘区域,但实际上,这是由 H1 蜡烛采样的随机漫步图表。 在此处,每个下一步骤向上或向下移动的概率为 50%,并且不取决于上一个步骤的方向。 在发展趋势的概念时,我将采用随机漫步作为基础,因为正如我先前所写,在这种情况下,预期收益为 0。 这是由于在此处每个下一步变化或保持其方向的可能性为 50%。 无论持仓持续了多少步,平均亏损始终等于平均利润。 猜测方向的概率也为 50%。 因此,我将假定随机漫步图表既非基于趋势,也非基于横盘。 它就是随机的。
现在我们有了一个样本,可以将价格序列与之进行比较,同时判定该价格序列是基于趋势还是横盘。
图例 2 示意由 H1 蜡烛采样的随机漫步图表。 这样的表达不太直观,并且会扭曲过程感知。 我们来研究一下显示图例 3 的源代码。 我已将该序列以 CSV 格式附加于下。 您可以在终端中下载它。
图例 3
图例 3 示意以 1 个点数为步长的随机漫步图表,以及以 1 个点数为大小的块形示意相同的漫步。 这些砖形令步骤可视性更佳。 在所有其他方面,图表相同。 由于我们假设随机漫步是定义价格序列趋势性质的参考,因此我们构建随机漫步增量概率密度分布图,从而将实际价格序列与参考进行比较。 此问题的解析可采用高斯函数来解决。 然而,解决方案不是那么直观。 即使是精通数学的人才,也可能无法完全理解每种所获分布形式的含义。 为了构建参考概率密度,我将采用组合规则,并构建一个表格。 其片段如图例 4 所示。 完整的 Excel 表附于文后。
图例 4
该表可令我们评估随机漫步在 40 步内可能垂直走了多远。 该 qs 比率(在表格的方程式中)允许设置构建表格的样本数量。 在示例当中,该表格已构建 100,000 个样本。 “vertical steps” 列含有垂直移动的步数,而 “probability of event %” 列显示这些垂直步骤的频率。 例如,该过程总共执行 40 个步骤,可以向上或向下执行 40 个步骤,我们有 100,000 个样本(度量)。 平均而言,该过程将 100,000 中的 40 个垂直步骤移动 0.00000009 次。 38 步进行0.0000036 次,而在 100,000 中进行 36 步进行 0.00007 次。 因此,在 “probability of event %” 列中设置数值数组,我们可以构建如图例 5 所示的增量概率密度分布图。
图例 5
该表格令我们能够获得 40 个步骤的参考增量概率密度分布,该过程每个后续步骤其方向发生变化和持续的概率等于 50%。 为了确保一切正确,我们可以测量随机漫步的概率密度分布,并将其与参考值进行比较。 针对随机漫步进行测量,其片段显示在图例 2 和 3 当中。 我将测量该功能在 40 个步骤和 100,000 个样本(度量)中进行了多少个垂直步骤。 结果如图例 6 所示。 Х 轴显示 -40...0...40 垂直步骤的幅度,而 Y 轴指定每个垂直步骤的事件数。
图例 6
每 40 步 100,000 个样本的参考分布(根据表格计算)以红色显示,而白色直方图则显示了所生成的随机漫步的实际测量的 100,000 个样本。 正如我们所见,参考分布和直方图几乎相同。 偏差很小。 我们取用的样本越多,实际测量值将与参考值相对准确。 现在,我们可以定义序列分布与参考分布之间的差异。 考虑到增量概率分布,我目前可以假设所分析序列尽可能准确地匹配随机漫步。 稍后我将解释为什么这样做是必要的。
为了执行测量,我们取用实际的 GBPUSD 图表,并将其转换为大小 0.00022 的砖形图表。 如以上示例所示,取用 100,000 个样本计算价格在 40 步中垂直移动了多少,并将其与图例 7 中的参考进行比较。
图例 7
如前所述,参考分布以红色显示,而测得的分布以白色显示。 现在,我需要简化之前我曾介绍的(用组合函数代替高斯函数)。 我们可以看到,GBPUSD 增量的分布相对于零轴是对称的。 相对于零轴的对称性则表明没有明显的向上或向下趋势。 这意味着每个上升砖形后随下降砖形的概率,与每个下降砖形后随上升砖形的概率相等。 换言之,价格走势没有单边向上或向下的明显倾向。
GBPUSD 分布图相比参考值更低且更宽、更有趣。 这表明,在 40 步内,价格通过零轴的频率比随机漫步的频率要少得多,并且通常在垂直方向上通过的砖形数量要多得多。 这意味着每个下一步其方向变化的概率略小于 50%。 该图形表明,一个上升砖形后随另一个上升砖形的概率超过 50%,一个下降砖形后随另一个下降砖形的概率也超过 50%。
这对我们有什么用? 我们回想一下期望收益方程,它令我们能够评估利润。 盈利的整个问题是,如果“正确”入场的概率大于 50%,那么只要平均亏损等于平均利润,我们则会继续保持盈利。 为了赚钱,我们需要打破 “50% 平衡”。 目前,我尚未评估确切的逆转概率。 可以依据该图进行计算,但如果我们假设该图的延续概率为 55%,而逆转概率为 45%,且平均利润与平均亏损相匹配,并等于 10 步(步长 0.00022*10=0.0022),那么预期收益 m=(55*0.0022)-(45*0.0022)=0.121-0.099=0.022。 反过来,这意味着完成 100 笔交易后,我们将保持 0.022 的利润。 如果我们针对 GBPUSD 交易 0.1 手,这意味着 $220 的利润。
知道趋势延续概率超过 50%,我们可以采用趋势延续策略,即在上涨之后买入。 换言之,如果趋势持续概率超过 50%,我们应采用顺势策略,并可获得利润。 反之,如果我们知道逆转概率大于 50%(上升砖形通常后随下跌砖形),则每次上升砖形收盘之后,我们都会建立一笔空头持仓,并可采用横盘(逆势)策略获利。
趋势/扁平定义直接取决于我们在特定行情中采用的获利策略。 如果在随机漫步的情况下,趋势延续概率为 50%,并且随机漫步既非基于趋势,也非基于横盘,则:
在趋势走势的情况下,趋势持续的概率超过趋势逆转的概率。 如果价格移动 10 个点,那么它将在同一方向上再次移动 10 个点的概率超过 50%。
在横盘走势的情况下,趋势逆转的概率超过趋势延续的概率。 如果价格移动 10 点,那么它将逆转,并向相反的方向再移动 10 点,其概率超过 50%。
如果价格以砖形显示(如上所述),且每个砖形 10 点,则趋势走势建议在每个后续上升砖形收盘后开仓做多,在每个后续下降砖形之后开仓做空。 反之,横盘走势建议在每个上升砖形之后开仓做空,在每个下降砖形之后开仓做多。
换句话说,如果行情处于趋势中,只需顺势交易。 如果行情处于横盘,则逆势交易。 如果行情既没有趋势,也非横盘,则不要入场。
在此,我并不是说随机漫步是不能赚钱的。 这是一个单独且彻底研究的主题。
看似符合逻辑的陈述有时被证明是错误的。 如此,我们用一个简单的模型来验证结论。 为此,创建 2 个过程,逆转概率分别为 80%(图例 8)和 20%(图例 9)。
图例 8
图例 9
图例 8 示意测量所得的概率密度分布比之参考范围窄得多。 该过程更频繁地回归零轴。 图例 9 示意测量所得的概率密度分布比之参考范围宽得多。 该过程回归零轴比平常要少许多。 故此,我们可以得出结论,先前执行的操作是正确的,逻辑也是如此。 如果逆转概率小于 50%,则表明分布比参考范围更宽,然后可将此逻辑运用到分析特定产品的趋势程度。 在此,我将介绍“趋势”的概念,该概念定量反映了延续趋势的过程倾向。
有了参考值,我们就可采用绝对值来估计一种产品的不同时间帧之间,和不同产品之间的趋势程度。 但首先我们要开发一种比较绝对值的方法。 我建议两种方法:
有了这样的工具,我们可以直接比较一种产品在不同规模(时间帧)上的趋势度,并直观地评估其统计参数。 作为示例,我们采用 20% 和 80% 逆转概率的 2 个相同过程,并以不同的比例直观地评估其统计参数。 以前,我采用的砖形大小等于 1 个点。 现在,我将创建更大尺寸的砖形,每个后续砖形的大小乘以 1.1 的比率。 因此,我将得到若干个尺度,其砖形大小为 1; 1.1; 1.21; 1.33 ..... 6.12. 图例 10 示意含有 80% 逆转概率的趋势如何随过程规模的增加而变化。 图例 11 示意对于 20% 逆转概率,该过程结果相同。
图例 10
图例 11
在图例 10 和 11 当中,最小比例尺(1 个点数)位于 X 轴的左侧,而最大比例尺位于 X 轴的右侧。 Y 轴含有采用“平均幅度”计算得出的金融产品趋势度。 在图例 10 之中,最初 80% 的逆转概率过程是横盘,第一直方图列的趋势性较低,但是随着比例的增加,趋势度趋向于 1(参考随机漫步值)。 这表明,尽管最小规模上的逆转概率很高,但对于较大的规模而言,情况却并非如此,因为该过程会丢失“记忆”,并变成随机漫步。 图例 11 示意类似的图片。 如果该过程最初的趋势高度为 2.053,则它会减少,并在更大规模内趋于随机漫步参考值。
图例 10 和 11 展示该过程仅在最小规模上具有“记忆”,且随着规模的增加而变得越来越像随机漫步。 该结论得到序列创建的支持。 当生成这两个过程时,仅考虑前一步的方向。 其余步骤并未考虑在内,因此“记忆”效应随着规模的增加而迅速消失。
真实行情不同于综合生成的序列。 检测形态需要更多的分析工具。 因此,不仅要分析固定步数的趋势度,而且要评估行情趋势如何随着经历的步数增加而变化。 由于参考表格可针对不同数量的步骤构建,我们不仅可以同步查看工具随着步长的增加如何运行,还可以查看当步数增加时其行为。 图例 12 示意 10,000 个样本的 GBPUSD 趋势度的动态变化,其砖形大小为 0.00314,步数为 10 到 100。 最左侧的直方图列已构建 10 步,而最右侧的直方图列则构建了 100 步。 每根直方柱列,步数按 2 递增。
图例 12
根据图例 12,在当前规模上,GBPUSD 趋势超过 1,并在 1.133-1.166 范围内波动,具体取决于执行分析的步骤数。 图例 13 示意趋势度如何随着规模的增加而变化。 该图形已针对 10,000 个样本构建,每个样本 40 个步骤,步长范围为 0.00021 至 0.00495。 最左侧的直方柱以砖形大小 0.00021 建立,而每根后续直方柱均超过了前一根 1.1 倍。
图例 13
图例 13 示意趋势度如何随着规模的增加而下降。 虽然最小比例等于 1.425,但已经趋向于 1,最大比例等于 1.062。 当规模增加时,GBPUSD 的行为与具有 20% 概率的合成序列的行为更相似。
这种方法令我们能够动态评估交易的金融产品趋势度的变化速度。 下面的动画展示 AMD 股价相对于参考分布的增量概率密度分布的动态。 以 M1 时间帧蜡烛作为基础。 该动画针对 40 个步骤,1000 个样本而构建的。 砖形大小根据当前的平均波动率动态变化。
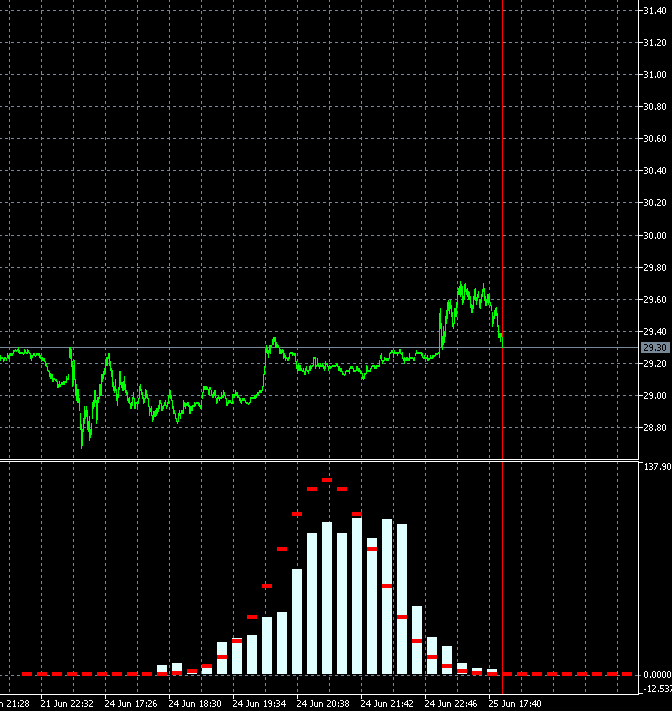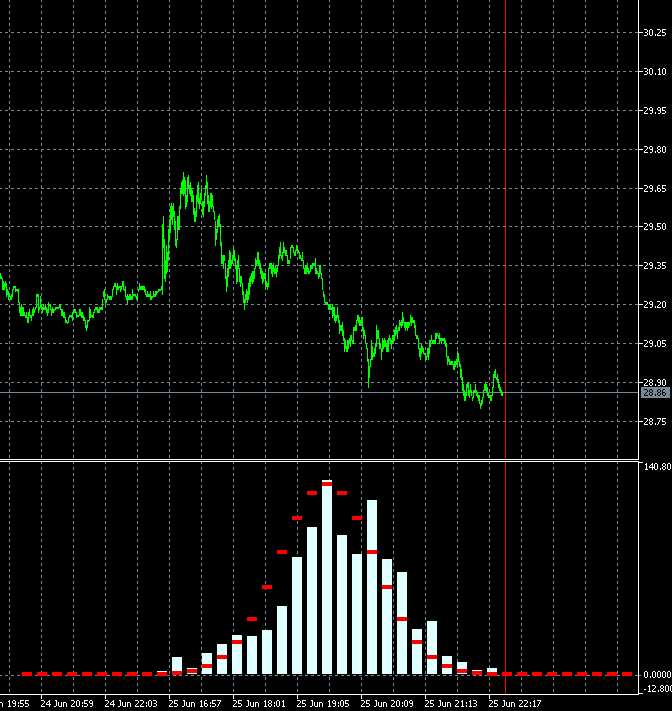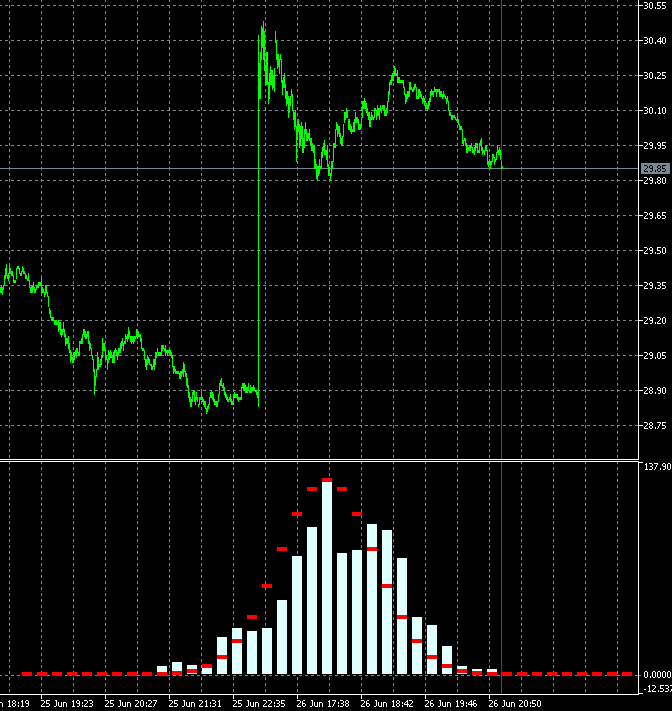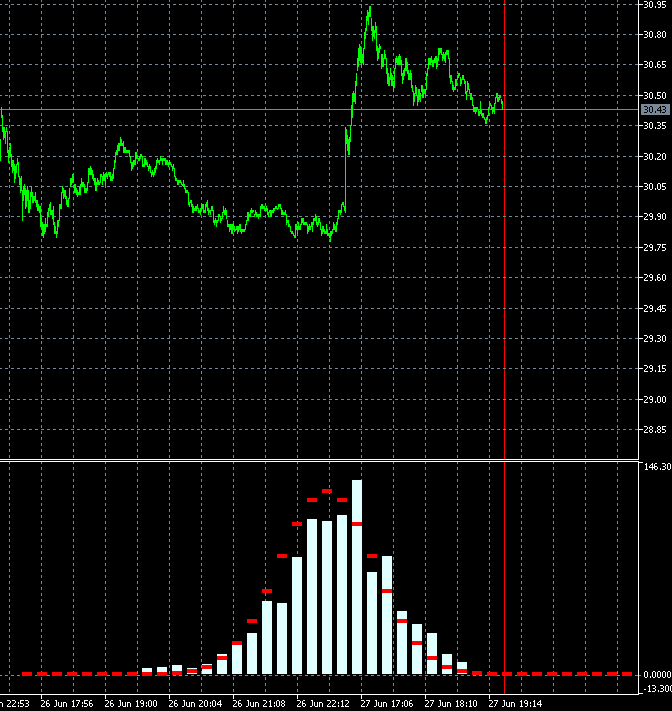
与 GBPUSD 不同,AMD 股价增量概率密度的分布并非零轴对称。 明显存在上升趋势分量。 这意味着与向下步骤后随向下步骤的情况相比,当向上步骤后随向上步骤时,趋势持续的概率略高。 这意味着在这种产品上进行做多交易更为合理。 在这种情况下,即便随机入场也可以保持盈利。
考虑到上述所有问题,我们可能会问一个问题,即行情主要是趋势、横盘还是随机的。 回答问题将令我们能够定义要应用的策略和分析。 我已分析了 30 多个货币对,50 多支俄罗斯和美国股票。 市场,以及加密货币和大宗商品市场。 大宗商品市场包括贵金属、能源和食品。 基于我的研究,我可以得出以下结论:
此处我们可以得出更宽泛的结论,但这是另一篇文章的主题。
以下是一些描述交易金融产品特征的图表。
为什么一种金融产品在较小的规模上更具倾向性,而在较大的规模上却更平稳? 在下一篇文章中,我将尝试解释这种行为的原因。 我会基于当前的研究开发算法,看看它是否能盈利。
趋势和横盘的概念可以清晰、完整地定义。 此外,可以比较不同金融产品,以及单个金融产品在不同规模上的趋势度。 这种分析令我们能够评估金融产品的特征和特性,并考虑每种金融产品的独特行为来构造交易算法。
了解金融产品的统计特性,及其随时间的变化,我们可以在开发交易算法时摆脱优化参数的烦恼。 取而代之,我们可以执行度量,并依据交易金融产品的统计特性有意识地修改交易算法参数。
以下是 20%,50% 和 80% 概率逆转图形的历史记录的文件。 此外,还有一个构建参考分布的 Excel 文件,以及为了分析构建砖形的指标。
指标算法由 Maxim Romanov 开发,指标代码由 Konstantin Gruzdev 创建。

本社区仅针对特定人员开放
查看需注册登录并通过风险意识测评
5秒后跳转登录页面...